(本小题12分)如图,已知直角梯形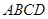 中,
中, 且
且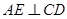 ,又
,又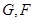 分别为
分别为 的中点,将△
的中点,将△ 沿
沿 折叠,使得
折叠,使得 .
.
(Ⅰ)求证:AE⊥平面CDE;
(Ⅱ)求证:FG∥平面BCD;
(Ⅲ)在线段AE上找一点R,使得平面BDR⊥平面DCB, 并说明理由.
推荐套卷
(本小题12分)如图,已知直角梯形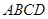 中,
中, 且
且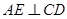 ,又
,又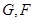 分别为
分别为 的中点,将△
的中点,将△ 沿
沿 折叠,使得
折叠,使得 .
.
(Ⅰ)求证:AE⊥平面CDE;
(Ⅱ)求证:FG∥平面BCD;
(Ⅲ)在线段AE上找一点R,使得平面BDR⊥平面DCB, 并说明理由.