如图,在三棱锥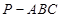 中,△PAB和△CAB都是以AB为斜边的等腰直角三角形, 若
中,△PAB和△CAB都是以AB为斜边的等腰直角三角形, 若 ,D是PC的中点
,D是PC的中点
(1)证明: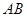

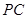 ;
;
(2)求AD与平面ABC所成角的正弦值.
如图,在三棱锥 中,底面△
中,底面△ 是边长为
是边长为 的等边三角形,
的等边三角形, ,
, 分别为
分别为 的中点,且
的中点,且 ,
, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
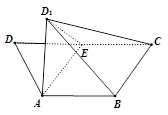
(本小题满分15分)已知四边形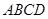 中,
中,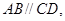
 ,
, 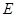 为
为 中点,连接
中点,连接 ,将
,将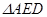 沿
沿 翻折到
翻折到 ,使得二面角
,使得二面角 的平面角的大小为
的平面角的大小为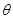 .
.
(Ⅰ)证明: ;
;
(Ⅱ)已知二面角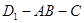 的平面角的余弦值为
的平面角的余弦值为 ,求
,求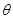 的大小及
的大小及 的长.
的长.
如图,正四棱锥 中,
中, ,
, 分别为
分别为 的中点,设
的中点,设 为线段
为线段 上任意一点。
上任意一点。
(Ⅰ)求证: ;
;
(Ⅱ)当直线 与平面
与平面 所成的角取得最大值时,求二面角
所成的角取得最大值时,求二面角 的平面角的余弦值.
的平面角的余弦值.
(本小题满分15分)如图,已知 平面
平面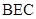 ,
, ,
, ,
, ,
,
为等边三角形.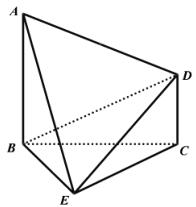
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
如图,弧 是半径为
是半径为 的半圆,
的半圆, 为直径,点
为直径,点 为弧
为弧 的中点,点
的中点,点 和点
和点 为线段
为线段 的三等分点,平面
的三等分点,平面 外一点
外一点 满足
满足 ,
, .
.
(Ⅰ)证明: ;
;
(Ⅱ)已知点 ,
, 为线段
为线段 ,
, 上的点,使得
上的点,使得 ,求当
,求当 最短时,平面
最短时,平面 和平面
和平面 所成二面角的正弦值.
所成二面角的正弦值.
如图,已知四棱锥S-A BCD是由直角梯形沿着CD折叠而成,其中SD=DA=AB=BC=l,AS∥BC,A⊥AD,且二面角S-CD-A的大小为120o.
(Ⅰ)求证:平面ASD⊥平面ABCD;
(Ⅱ)设侧棱SC和底面ABCD所成角为 ,求
,求 的正弦值.
的正弦值.
如图,三棱锥P-ABC中,E,D分别是棱BC,AC的中点,PB="PC=AB=4,AC=8," BC= ,PA=
,PA= .
.
(Ⅰ)求证:BC⊥平面PED;
(Ⅱ)求直线AC与平面PBC所成角的正弦值.
如图,在四棱锥 中,底面
中,底面 为直角梯形,且
为直角梯形,且 ,
, ,侧面
,侧面 底面
底面 . 若
. 若 .
.
(1)求证: 平面
平面 ;
;
(2)侧棱 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,指出点
?若存在,指出点 的位置并证明,若不存在,请说明理由;
的位置并证明,若不存在,请说明理由;
(3)求二面角 的余弦值.
的余弦值.
如图,平面 平面
平面 ,四边形
,四边形 是边长为2的正方形,
是边长为2的正方形, 为
为 上的点,且
上的点,且 平面
平面 .
.
(1)求证 平面
平面 ;
;
(2)设 ,是否存在
,是否存在 ,使二面角
,使二面角 的余弦值为
的余弦值为 ?若存在,求
?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
如图,三棱锥
中,平面
平面
,
,点
在线段
上,且
,点
在线段
上,且
.

(Ⅰ)证明:
平面
.
(Ⅱ)若四棱锥
的体积为7,求线段
的长.
如图,在三棱锥 中,
中, 底面
底面 ,
, ,
, 为
为 的中点,
的中点,  为
为 的中点,
的中点, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求 与平面
与平面 成角的正弦值;
成角的正弦值;
(3)设点 在线段
在线段 上,且
上,且 ,
, 平面
平面 ,求实数
,求实数 的值.
的值.
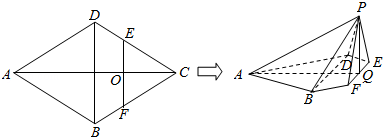
如图所示,在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,EF∩AC=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到五棱锥P﹣ABFED,且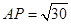 ,PB=
,PB= .
.
(1)求证:BD⊥平面POA;
(2)求二面角B﹣AP﹣O的正切值.