浙江省金华十校高三下学期高考模拟（4月）文科数学试卷

设集合S={x∈N|0<x<6}，T={4,5,6}，则S∩T =

已知a,b∈R，则 “a>b”是“a>b-1”成立的

若三棱锥的三视图如右图所示，则该三棱锥的体积为

A．80

B．40

C．

D．

设等差数列{a_n}的前n项和为S_n，且满足S₁₉>0，S₂₀<0，则使S_n取得最大项的n为

若m、n是两条不同的直线，a、b、g是三个不同的平面，则下列命题中为真命题的是

已知函数f（x）=log_a（2^x+b-1）的部分图像如图所示，则a，b所
满足的关系为

已知F₁、F₂为双曲线C：的左、右焦点，P为双曲线C右支上一点，且PF₂⊥F₁F₂，
PF₁与y轴交于点Q，点M满足，若MQ⊥PF₁，则双曲线C的离心率为

A．

B．

C．

D．

已知函数f（x）=的最大值和最小值分别是M，m，则M•m为

函数f（x）=lg（9-x²）的定义域为____，单调递增区间为____，3f（2）+f（1） =   ．

已知直线l₁：ax+2y+6=0，l₂：x+（a-1）y+a²-1=0，若l₁⊥l₂，则a=        ，若 l₁∥l₂，则a=     ，此时l₁和l₂之间的距离为    ．

设w>0，函数的图象向左平移个
单位后，得到右边的图像，则w=      ，j=      ．

已知实数x,y满足，此不等式组表示的平面区域的面积为     ，目标函数Z=2x-y的最小值为    ．

如图，在正三棱柱ABC-A₁B₁C₁中，D为AB的中点，AA₁=4，AB=6，则异面直线B₁D与AC₁所成角的余弦值为     ．

已知三角形ABC的三个顶点都在椭圆上，且AB⊥x轴，AC∥x轴，则的最大值为     ．

在△ABC中，AB=BC=2，AC=3．设O是△ABC的内心，若，则的值为     ．

在△ABC中，分别是的对边长，已知．
（Ⅰ）若，求实数的值;
（Ⅱ）若,求△ABC面积的最大值．

如图，三棱锥P-ABC中，E,D分别是棱BC,AC的中点，PB="PC=AB=4,AC=8," BC=,PA=．

（Ⅰ）求证：BC⊥平面PED；
（Ⅱ）求直线AC与平面PBC所成角的正弦值．

设S_n为等差数列{a_n}的前n项和，其中a₁=1，且（ n∈N*）．
（Ⅰ）求常数的值，并写出{a_n}的通项公式；
（Ⅱ）记，数列{b_n}的前n项和为T_n，若对任意的n≥2，都有成立，求的取值范围．

已知抛物线C：y²=2px（p>0），曲线M：x²+2x+y²=0（y>0）．过点P（-3,0）与曲线M相切于点A的直线l，与抛物线C有且只有一个公共点B．
 
（Ⅰ）求抛物线C的方程及点A，B的坐标；
（Ⅱ）过点B作倾斜角互补的两条直线分别交抛物线C于S，T两点（不同于坐标原点），求证：直线ST∥直线AO．

巳知二次函数f（x）=ax²+bx+c （a>0，b，c∈R）．
（Ⅰ）已知a=2，f（2）=2，若f（x）≥2对x∈R恒成立，求f（x）的表达式；
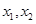（Ⅱ）已知方程f（x）=0的两实根 满足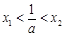 ．设f（x）在R上的最小值为m，求证：m<x₁．