已知抛物线C：y2=2px（p>0），曲线M：x2+2x+y2=0（y>0）．过点P（-3,0）与曲线M相切于点A的直线l，与抛物线C有且只有一个公共点B．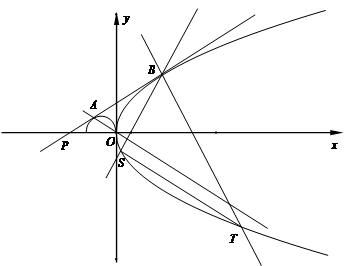
（Ⅰ）求抛物线C的方程及点A，B的坐标；
（Ⅱ）过点B作倾斜角互补的两条直线分别交抛物线C于S，T两点（不同于坐标原点），求证：直线ST∥直线AO．
满足：
令
表示成
的不含
（即写出
的解析式），
时，求函数
的定义域为
，
的定义域为
。
，求
、
的取值范围。
，求函数
的值域.
的解集为
，求不等式
的解集。
的不等式
的解集为
，不等式
的解集为
．
，求
，求正数
的取值范围．相关知识点
推荐套卷
已知抛物线C：y2=2px（p>0），曲线M：x2+2x+y2=0（y>0）．过点P（-3,0）与曲线M相切于点A的直线l，与抛物线C有且只有一个公共点B．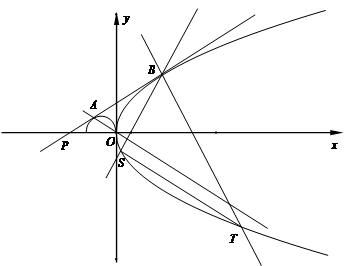
（Ⅰ）求抛物线C的方程及点A，B的坐标；
（Ⅱ）过点B作倾斜角互补的两条直线分别交抛物线C于S，T两点（不同于坐标原点），求证：直线ST∥直线AO．
粤公网安备 44130202000953号