某班主任对全班50名学生进行了作业量多少的调查，喜欢玩电脑游戏的同学认为作业多的有18人，认为作业不多的有9人，不喜欢玩电脑游戏的同学认为作业多的有8人，认为作业不多的有15人.
（1）根据以上数据建立一个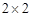
的列联表；
（2）认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少？(参考数值：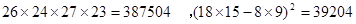
)
满足
，
，求
．
满足
，且
，求
．
}满足a
=1，
,求数列{a
}满足a
=1，a
a
+1（n≥2），求数列{a
前n项和
.
与
的关系；（2）求通项公式相关知识点
推荐套卷
某班主任对全班50名学生进行了作业量多少的调查，喜欢玩电脑游戏的同学认为作业多的有18人，认为作业不多的有9人，不喜欢玩电脑游戏的同学认为作业多的有8人，认为作业不多的有15人.
（1）根据以上数据建立一个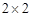的列联表；
（2）认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少？(参考数值： )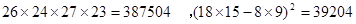
粤公网安备 44130202000953号