已知数列{an}中,a1= ,an+1=
,an+1= (n∈N*).
(n∈N*).
(1)求证:数列{ }是等差数列,并求{an}的通项公式;
}是等差数列,并求{an}的通项公式;
(2)设bn+an=l(n∈N*),S=b1b2+b2b3+…+bnbn+1,试比较an与8Sn的大小.
(本小题满分12分)数列 中,已知
中,已知 ,
, 时,
时, .数列
.数列 满足:
满足: .
.
(Ⅰ)证明: 为等差数列,并求
为等差数列,并求 的通项公式;
的通项公式;
(Ⅱ)记数列 的前
的前 项和为
项和为 ,是否存在正整数
,是否存在正整数 ,使得
,使得 成立?若存在,求出所有符合条件的有序实数对
成立?若存在,求出所有符合条件的有序实数对 ;若不存在,说明理由.
;若不存在,说明理由.
是否存在一个等比数列 同时满足下列三个条件:
同时满足下列三个条件:
① 且
且 ;
;
② ;
;
③至少存在一个 ,使得
,使得 依次构成等差数列?若存在,求出通项公式;若不存在,说明理由.
依次构成等差数列?若存在,求出通项公式;若不存在,说明理由.
已知数列 的前
的前 项和
项和 ,数列
,数列 满足
满足 .
.
(1)求
(2)求证数列 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
(3)设 ,数列
,数列 的前
的前 项和为
项和为 ,求满足
,求满足 的
的 的最大值.
的最大值.
已知数列{an}的前n项和 ,数列{bn}满足b1=1,b3+b7=18,且
,数列{bn}满足b1=1,b3+b7=18,且 (n≥2).(1)求数列{an}和{bn}的通项公式;(2)若
(n≥2).(1)求数列{an}和{bn}的通项公式;(2)若 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
设数列
的前
项和为
.若对任意的正整数
,总存在正整数
,使得
,则称
是"
数列".
(1)若数列
的前
项和为
,证明:
是"
数列".
(2)设
是等差数列,其首项
,公差
,若
是"
数列",求
的值;
(3)证明:对任意的等差数列
,总存在两个"
数列"
和
,使得
成立.
已知数列{an}的前n项和Sn=-an- n-1+2(n∈N*),数列{bn}满足bn=2nan.
n-1+2(n∈N*),数列{bn}满足bn=2nan.
(1)求证数列{bn}是等差数列,并求数列{an}的通项公式.
(2)设数列 的前n项和为Tn,证明:n∈N*且n≥3时,Tn>
的前n项和为Tn,证明:n∈N*且n≥3时,Tn> .
.
(3)设数列{cn}满足an(cn-3n)=(-1)n-1λn(λ为非零常数,n∈N*),问是否存在整数λ,使得对任意n∈N*,都有cn+1>cn.
已知数列{an}的前n项和为Sn,且Sn=2an-2(n∈N*),数列{bn}满足b1=1,且点P(bn,bn+1)(n∈N*)在直线y=x+2上.
(1)求数列{an},{bn}的通项公式.
(2)求数列{an·bn}的前n项和Dn.
(3)设cn=an·sin2 -bn·cos2
-bn·cos2 (n∈N*),求数列{cn}的前2n项和T2n.
(n∈N*),求数列{cn}的前2n项和T2n.
已知首项为
的等比数列
不是递减数列,其前
项和为
,且
成等差数列.
(1)求数列
的通项公式;
(2)设
,求数列
的最大项的值与最小项的值.
给定正整数 ,若项数为
,若项数为 的数列
的数列 满足:对任意的
满足:对任意的 ,均有
,均有 (其中
(其中 ),则称数列
),则称数列 为“Γ数列”.
为“Γ数列”.
(1)判断数列 和
和 是否是“Γ数列”,并说明理由;
是否是“Γ数列”,并说明理由;
(2)若 为“Γ数列”,求证:
为“Γ数列”,求证: 对
对 恒成立;
恒成立;
(3)设 是公差为
是公差为 的无穷项等差数列,若对任意的正整数
的无穷项等差数列,若对任意的正整数 ,
,
均构成“Γ数列”,求 的公差
的公差 .
.
已知函数 , 数列
, 数列 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)令 ,若
,若 对一切
对一切 成立,求最小正整数m.
成立,求最小正整数m.
已知函数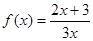 , 数列
, 数列 满足
满足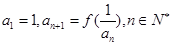 .
.
(1)求数列 的通项公式;
的通项公式;
(2)令 ,若
,若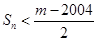 对一切
对一切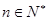 成立,求最小正整数m.
成立,求最小正整数m.