·广东理)设数列 的前
的前 项和为
项和为 .已知
.已知 ,
, ,
, .
.
(1) 求 的值;
的值;
(2) 求数列 的通项公式;
的通项公式;
(3) 证明:对一切正整数 ,有
,有 .
.
已知首项为 的等比数列
的等比数列 不是递减数列,其前n项和为
不是递减数列,其前n项和为 ,且
,且 成等差数列。
成等差数列。
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的最大项的值与最小项的值。
的最大项的值与最小项的值。
已知等差数列{an}的前n项和为Sn,S7=49,a4和a8的等差中项为2.
(1)求an及Sn;
(2)证明:当n≥2时,有 .
.
已知等差数列 的首项
的首项 ,公差
,公差 ,且
,且 、
、 、
、 分别是等比数列
分别是等比数列 的
的 、
、 、
、 .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设数列 对任意正整数
对任意正整数 均有
均有 成立,求
成立,求 的值.
的值.
在数列{an}中, ,
,
 ,
,
(1)求数列 的通项公式
的通项公式
(2)设 (
( ),记数列
),记数列 的前k项和为
的前k项和为 ,求
,求 的最大值.
的最大值.
已知数列 的各项均为正数,其前
的各项均为正数,其前 项和为
项和为 ,且
,且 ,
, ,数列
,数列 是首项和公比均为
是首项和公比均为 的等比数列.
的等比数列.
(1)求证数列 是等差数列;
是等差数列;
(2)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知数列 中,
中, ,对任意的
,对任意的 ,
, 、
、 、
、 成等比数列,公比为
成等比数列,公比为 ;
; 、
、 、
、 成等差数列,公差为
成等差数列,公差为 ,且
,且 .
.
(1)写出数列 的前四项;
的前四项;
(2)设 ,求数列
,求数列 的通项公式;
的通项公式;
(3)求数列 的前
的前 项和
项和 .
.
设 是各项均不为零的
是各项均不为零的 (
( )项等差数列,且公差
)项等差数列,且公差 .
.
(1)若 ,且该数列前
,且该数列前 项和
项和 最大,求
最大,求 的值;
的值;
(2)若 ,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求
,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求 的值;
的值;
(3)若该数列中有一项是 ,则数列
,则数列 中是否存在不同三项(按原来的顺序)为等比数列?请说明理由.
中是否存在不同三项(按原来的顺序)为等比数列?请说明理由.
(本小题满分13分)
已知数列 ,设
,设  ,数列
,数列 .
.
(I)求证: 是等差数列;
是等差数列;
(II)求数列 的前n项和Sn;
的前n项和Sn;
(Ⅲ)若 一切正整数n恒成立,求实数m的取值范围.
一切正整数n恒成立,求实数m的取值范围.
设等差数列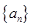 的公差为
的公差为 ,且
,且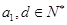 .若设
.若设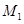 是从
是从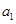 开始的前
开始的前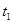 项数列的和,即
项数列的和,即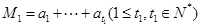 ,
,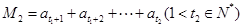 ,如此下去,其中数列
,如此下去,其中数列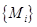 是从第
是从第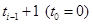 开始到第
开始到第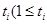 )项为止的数列的和,即
)项为止的数列的和,即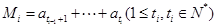 .
.
(1)若数列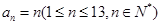 ,试找出一组满足条件的
,试找出一组满足条件的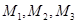 ,使得:
,使得:  ;
;
(2)试证明对于数列 ,一定可通过适当的划分,使所得的数列
,一定可通过适当的划分,使所得的数列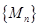 中的各数都为平方数;
中的各数都为平方数;
(3)若等差数列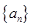 中
中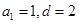 .试探索该数列中是否存在无穷整数数列
.试探索该数列中是否存在无穷整数数列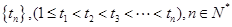 ,使得
,使得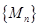 为等比数列,如存在,就求出数列
为等比数列,如存在,就求出数列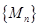 ;如不存在,则说明理由.
;如不存在,则说明理由.
已知各项均不相等的等差数列 的前四项和
的前四项和 成等比.
成等比.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,若
,若 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
为了保障幼儿园儿童的人身安全,国家计划在甲、乙两省试行政府规范购置校车方案,计划若干时间内(以月为单位)在两省共新购1000辆校车.其中甲省采取的新购方案是:本月新购校车10辆,以后每月的新购量比上一月增加50%;乙省采取的新购方案是:本月新购校车40辆,计划以后每月比上一月多新购m辆.
(1)求经过n个月,两省新购校车的总数S(n);
(2)若两省计划在3个月内完成新购目标,求m的最小值.
正实数数列{an}中,a1=1,a2=5,且{ }成等差数列.
}成等差数列.
(1)证明:数列{an}中有无穷多项为无理数;
(2)当n为何值时,an为整数?并求出使an<200的所有整数项的和.