(本题满分16分)本题共3小题,第(1)小题4分,第(2)小题4分,第(3)小题8分.
已知数列 是公差不为
是公差不为 的等差数列,
的等差数列, 数列
数列 是等比数列,且
是等比数列,且 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,记点
,记点 .
.
(1)求数列 的通项公式;
的通项公式;
(2)证明:点 在同一直线
在同一直线 上,并求出直线
上,并求出直线 方程;
方程;
(3)若 对
对 恒成立,求
恒成立,求 的最小值.
的最小值.
已知数列 的前
的前 项和为
项和为 ,且
,且 ,
, N*
N*
(1)求数列 的通项公式;
的通项公式;
(2)已知 (
( N*),记
N*),记
 (
(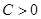 且
且 ),是否存在这样的常数
),是否存在这样的常数 ,使得数列
,使得数列 是常数列,若存在,求出
是常数列,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若数列 ,对于任意的正整数
,对于任意的正整数 ,均有
,均有 成立,求证:数列
成立,求证:数列 是等差数列;
是等差数列;
(本小题满分12分)已知等比数列{an}的公比 ,前n项和为Sn,S3=7,且
,前n项和为Sn,S3=7,且 ,
, ,
,
成等差数列,数列{bn}的前n项和为Tn, ,其中
,其中 N*.
N*.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{bn}的通项公式;
(Ⅲ)设 ,
, ,
, ,求集合C中所有元素之和.
,求集合C中所有元素之和.
已知等差数列 的前n项和为
的前n项和为 ,且
,且 .数列
.数列 的前n项和为
的前n项和为 ,且
,且 ,
, .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)设 , 求数列
, 求数列 的前
的前 项和
项和 .
.
已知函数 ,各项均不相等的有限项数列
,各项均不相等的有限项数列 的各项
的各项 满足
满足 .令
.令 ,
, 且
且 ,例如:
,例如: .
.
(Ⅰ)若 ,数列
,数列 的前n项和为Sn,求S19的值;
的前n项和为Sn,求S19的值;
(Ⅱ)试判断下列给出的三个命题的真假,并说明理由。
①存在数列 使得
使得 ;②如果数列
;②如果数列 是等差数列,则
是等差数列,则 ;
;
③如果数列 是等比数列,则
是等比数列,则 。
。
(本小题满分13分)已知等比数列 的公比
的公比 ,前n项和为
,前n项和为 且
且 成等差数列,数列
成等差数列,数列 的前n项和为
的前n项和为 ,其中
,其中 。
。
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的通项公式;
的通项公式;
(3)设 ,
, ,求集合
,求集合 中的所有元素之和。
中的所有元素之和。
已知数列 满足
满足 ,
, .
.
(1)求证:数列 是等差数列;
是等差数列;
(2)设 ,数列
,数列 的前
的前 项之和为
项之和为 ,求证:
,求证: .
.
(本小题满分14分)已知数列 满足
满足 ,
, ,
, .
.
(1)求证:数列 是等差数列;
是等差数列;
(2)求证: .
.
已知正项数列 ,
, ,且
,且
(1)求证: 是等差数列,并求
是等差数列,并求 的通项公式;
的通项公式;
(2)数列 满足
满足 ,若
,若 ,仍是
,仍是 中的项,求
中的项,求 在区间
在区间 中的所有可能值之和
中的所有可能值之和 ;
;
(3)若将上述递推关系 改为:
改为: ,且数列
,且数列 中任意项
中任意项 ,试求满足要求的实数
,试求满足要求的实数 的取值范围
的取值范围
已知数列 是等差数列,其前n项和为Sn,若
是等差数列,其前n项和为Sn,若 ,
, .
.
(1)求 ;
;
(2)若数列{Mn}满足条件:  ,当
,当 时,
时, -
- ,其中数列
,其中数列 单调递增,且
单调递增,且 ,
, .
.
①试找出一组 ,
, ,使得
,使得 ;
;
②证明:对于数列 ,一定存在数列
,一定存在数列 ,使得数列
,使得数列 中的各数均为一个整数的平方.
中的各数均为一个整数的平方.