已知数列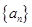 是等差数列,其前n项和为Sn,若
是等差数列,其前n项和为Sn,若 ,
,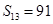 .
.
(1)求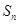 ;
;
(2)若数列{Mn}满足条件: 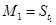 ,当
,当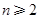 时,
时,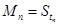 -
-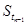 ,其中数列
,其中数列 单调递增,且
单调递增,且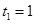 ,
,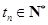 .
.
①试找出一组 ,
,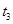 ,使得
,使得 ;
;
②证明:对于数列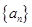 ,一定存在数列
,一定存在数列 ,使得数列
,使得数列 中的各数均为一个整数的平方.
中的各数均为一个整数的平方.
相关知识点
推荐套卷
已知数列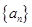 是等差数列,其前n项和为Sn,若
是等差数列,其前n项和为Sn,若 ,
,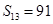 .
.
(1)求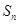 ;
;
(2)若数列{Mn}满足条件: 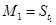 ,当
,当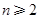 时,
时,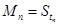 -
-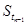 ,其中数列
,其中数列 单调递增,且
单调递增,且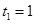 ,
,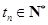 .
.
①试找出一组 ,
,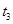 ,使得
,使得 ;
;
②证明:对于数列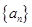 ,一定存在数列
,一定存在数列 ,使得数列
,使得数列 中的各数均为一个整数的平方.
中的各数均为一个整数的平方.