已知数列{an}中,a1=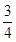 ,an+1=
,an+1= (n∈N*).
(n∈N*).
(1)求证:数列{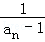 }是等差数列,并求{an}的通项公式;
}是等差数列,并求{an}的通项公式;
(2)设bn+an=l(n∈N*),S=b1b2+b2b3+…+bnbn+1,试比较an与8Sn的大小.
相关知识点
推荐套卷
已知数列{an}中,a1=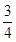 ,an+1=
,an+1= (n∈N*).
(n∈N*).
(1)求证:数列{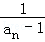 }是等差数列,并求{an}的通项公式;
}是等差数列,并求{an}的通项公式;
(2)设bn+an=l(n∈N*),S=b1b2+b2b3+…+bnbn+1,试比较an与8Sn的大小.