已知数列{an}的前n项和Sn＝－an－
n－1＋2(n∈N*)，数列{bn}满足bn＝2nan．
(1)求证数列{bn}是等差数列，并求数列{an}的通项公式．
(2)设数列
的前n项和为Tn，证明：n∈N*且n≥3时，Tn＞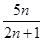
．
(3)设数列{cn}满足an(cn－3n)＝(－1)n－1λn(λ为非零常数，n∈N*)，问是否存在整数λ，使得对任意n∈N*，都有cn＋1＞cn．
转化为“十进制”数，再把它转化为“八进制”数.
＋
＋
＋…＋
的值，要求画出程序框图．相关知识点
推荐套卷
已知数列{an}的前n项和Sn＝－an－n－1＋2(n∈N*)，数列{bn}满足bn＝2nan．
(1)求证数列{bn}是等差数列，并求数列{an}的通项公式．
(2)设数列的前n项和为Tn，证明：n∈N*且n≥3时，Tn＞．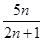
(3)设数列{cn}满足an(cn－3n)＝(－1)n－1λn(λ为非零常数，n∈N*)，问是否存在整数λ，使得对任意n∈N*，都有cn＋1＞cn．
粤公网安备 44130202000953号