（本小题满分13分）某种零件按质量标准分为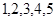
五个等级.现从一批该零件中随机抽取
个，对其等级进行统计分析，得到频率分布表如下：
| 等级 |
 |
 |
 |
 |
 |
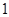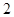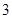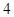| 频率 |
 |
 |
 |
 |
 |
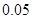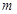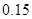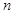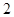（Ⅰ）在抽取的个零件中，等级为的恰有个，求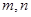
；
（Ⅱ）在（Ⅰ）的条件下，从等级为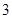和的所有零件中，任意抽取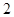个，求抽取的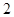个零
件等级恰好相同的概率.
相关知识点
推荐套卷
（本小题满分13分）某种零件按质量标准分为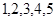五个等级.现从一批该零件中随机抽取个，对其等级进行统计分析，得到频率分布表如下：
| 等级 |
|
|
|
|
|
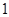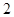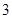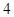| 频率 |
|
|
|
|
|
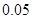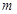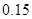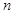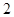（Ⅰ）在抽取的个零件中，等级为的恰有个，求；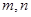
（Ⅱ）在（Ⅰ）的条件下，从等级为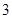和的所有零件中，任意抽取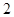个，求抽取的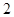个零
件等级恰好相同的概率.
粤公网安备 44130202000953号