定义:若 在
在 上为增函数,则称
上为增函数,则称 为“k次比增函数”,其中
为“k次比增函数”,其中 . 已知
. 已知 其中e为自然对数的底数.
其中e为自然对数的底数.
(1)若 是“1次比增函数”,求实数a的取值范围;
是“1次比增函数”,求实数a的取值范围;
(2)当 时,求函数
时,求函数 在
在 上的最小值;
上的最小值;
(3)求证: .
.
已知函数 ,其中
,其中 ,
, 是自然对数的底数.
是自然对数的底数.
(1)求函数 的零点;
的零点;
(2)若对任意 均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
(3)已知 ,且函数
,且函数 在R上是单调函数,探究函数
在R上是单调函数,探究函数 的单调性.
的单调性.
(本小题满分12分)已知函数 .
.
(1)判断 的奇偶性.
的奇偶性.
(2)判断 在
在 上的单调性,并用定义证明.
上的单调性,并用定义证明.
(3)是否存在实数 ,使不等式
,使不等式 对一切
对一切 恒成立?若存在,求出
恒成立?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧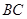 以及两条线段
以及两条线段 和
和 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 所在圆的半径为10米.设小圆弧
所在圆的半径为10米.设小圆弧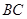 所在圆的半径为
所在圆的半径为 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.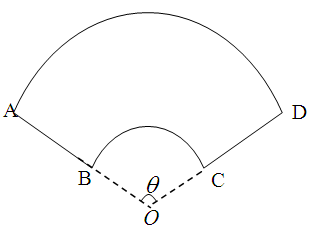
(1)求 关于
关于 的函数关系式;
的函数关系式;
(2)在对花坛的边缘进行装饰时,已知两条线段的装饰费用为4元/米,两条弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为 ,当
,当 为何值时,
为何值时, 取得最大值?
取得最大值?
已知函数
 .
.
(1)讨论函数 的奇偶性;
的奇偶性;
(2)若函数 在
在 上为减函数,求
上为减函数,求 的取值范围.
的取值范围.
设函数 的定义域为E,值域为F.
的定义域为E,值域为F.
(1)若E={1,2},判断实数λ=lg22+lg2lg5+lg5﹣ 与集合F的关系;
与集合F的关系;
(2)若E={1,2,a},F={0,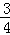 },求实数a的值.
},求实数a的值.
(3)若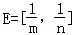 ,F=[2﹣3m,2﹣3n],求m,n的值.
,F=[2﹣3m,2﹣3n],求m,n的值.
【改编】函数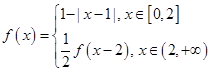 ,则下列命题中正确命题的个数是 ().
,则下列命题中正确命题的个数是 ().
①函数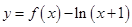 有
有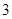 个零点;
个零点;
②若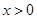 时,函数
时,函数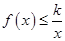 恒成立,则实数
恒成立,则实数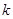 的取值范围是
的取值范围是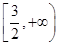 ;
;
③函数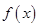 的极大值中一定存在最小值;
的极大值中一定存在最小值;
④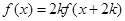
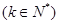 ,对一切
,对一切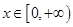 恒成立.
恒成立.
A.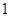 |
B.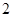 |
C.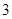 |
D.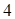 |
已知函数 .
.
(1)求函数 的最小值;
的最小值;
(2)已知 ,命题
,命题 :关于
:关于 的不等式
的不等式 对任意
对任意 恒成立;
恒成立; :函数
:函数 是增函数.若“
是增函数.若“ 或
或 ”为真,“
”为真,“ 且
且 ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
已知函数 是定义域为
是定义域为 的偶函数.当
的偶函数.当 时,
时, 若关于
若关于 的方程
的方程
 有且只有7个不同实数根,则
有且只有7个不同实数根,则 的值是.
的值是.
已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)证明:对任意的 ,存在唯一的
,存在唯一的 ,使
,使 ;
;
(3)设(2)中所确定的 关于
关于 的函数为
的函数为 ,证明:当
,证明:当 时,有
时,有 .
.
已知实数 ,函数
,函数 .
.
(1)当 时,求
时,求 的最小值;
的最小值;
(2)当 时,判断
时,判断 的单调性,并说明理由;
的单调性,并说明理由;
(3)求实数 的范围,使得对于区间
的范围,使得对于区间 上的任意三个实数
上的任意三个实数 ,都存在以
,都存在以 为边长的三角形.
为边长的三角形.
已知函数 的导数
的导数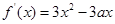 ,
,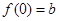 ,(a,b为实数),
,(a,b为实数),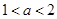 .
.
(1)若 在区间
在区间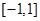 上的最小值、最大值分别为
上的最小值、最大值分别为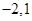 ,求a,b的值;
,求a,b的值;
(2)设函数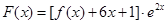 ,试判断函数
,试判断函数 的极值点个数.
的极值点个数.