若偶函数f(x)在(-∞,-1]上是增函数,则下列关系式中,成立的是()
A. <f(-1)<f(2) <f(-1)<f(2) |
B.f(-1)< <f(2) <f(2) |
C.f(2)<f(-1)< |
D.f(2)< <f(-1) <f(-1) |
已知f(x)=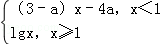 是(﹣∞,+∞)上的增函数,那么a的取值范围是()
是(﹣∞,+∞)上的增函数,那么a的取值范围是()
| A.(1,+∞) | B.(﹣∞,3) |
C.[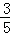 ,3) ,3) |
D.(1,3) |
下列判断正确的是 (把正确的序号都填上).
①若f(x)=ax2+(2a+b)x+2 (其中x∈[2a-1,a+4])是偶函数,则实数b=2;
②若函数 在区间
在区间 上递增,在区间
上递增,在区间 上也递增,则函数
上也递增,则函数 必在
必在 上递增;
上递增;
③f(x)表示-2x+2与-2x2+4x+2中的较小者,则函数f(x)的最大值为1;
④已知f(x)是定义在R上的不恒为零的函数,且对任意的x、y∈R都满足f(x·y)=x·f(y)+y·f(x),则f(x)是奇函数.Ks
函数y=ax2+bx+3在(-∞,-1]上是增函数,在[-1,+∞)上是减函数,则()
| A.b>0且a<0 | B.b=2a<0 | C.b=2a>0 | D.a,b的符号不定 |
已知偶函数f(x)在区间[0,+∞)单调递减,则满足f(lnx)>f(1)的x取值范围是()
A.( ,1) ,1) |
B.(0, )∪(1,+∞) )∪(1,+∞) |
C.( ,e) ,e) |
| D.(0,1)∪(e,+∞) |