设二次函数 .
.
(1)当 时,求函数
时,求函数 在
在 上的最小值
上的最小值 的表达式;
的表达式;
(2)若方程 有两个非整数实根,且这两实数根在相邻两整数之间,试证明存在整数
有两个非整数实根,且这两实数根在相邻两整数之间,试证明存在整数 ,使得
,使得 .
.
设函数 ,
, ,
, 为常数.
为常数.
(1)用 表示
表示 的最小值,求
的最小值,求 的解析式;
的解析式;
(2)在(1)中,是否存在最小的整数 ,使得
,使得 对于任意
对于任意 均成立,若存在,求出
均成立,若存在,求出 的
的
值;若不存在,请说明理由.
已知函数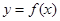 的定义域为
的定义域为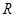 ,且对任意实数
,且对任意实数 恒有
恒有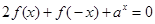
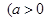 且
且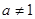 )成立.
)成立.
(Ⅰ)求函数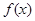 的解析式;
的解析式;
(Ⅱ)讨论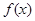 在
在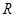 上的单调性, 并用定义加以证明.
上的单调性, 并用定义加以证明.
设函数 ,其中
,其中 .
.
(1)若 ,
, 的定义域为区间
的定义域为区间 ,求
,求 的最大值和最小值;
的最大值和最小值;
(2)若 的定义域为区间(0,+∞),求
的定义域为区间(0,+∞),求 的取值范围,使
的取值范围,使 在定义域内是单调减函数.
在定义域内是单调减函数.
已知函数f(x)=﹣xlnx+ax在(0,e)上是增函数,函数 .当x∈[0,ln3]时,函数g(x)的最大值M与最小值m的差为
.当x∈[0,ln3]时,函数g(x)的最大值M与最小值m的差为 ,则a= .
,则a= .
已知 为
为 上的偶函数,对任意
上的偶函数,对任意 都有
都有 且当
且当 ,
, 时,有
时,有 成立,给出四个命题:①
成立,给出四个命题:①  ;② 直线
;② 直线 是函数
是函数 的图像的一条对称轴;③ 函数
的图像的一条对称轴;③ 函数 在[-9,-6]上为增函数;④ 函数
在[-9,-6]上为增函数;④ 函数 在[-9,9]上有四个零点,其中所有正确命题的序号为 .
在[-9,9]上有四个零点,其中所有正确命题的序号为 .
设x∈R,对于使﹣x2+2x≤M成立的所有常数M中,我们把M的最小值1叫做﹣x2+2x的上确界.若a,b∈R+,且a+b=1,则 的上确界为()
的上确界为()
| A.﹣5 | B.﹣4 | C. |
D. |