某市政府欲在如图所示的矩形 的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形
的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形 (线段
(线段 和
和 为两条底边),已知
为两条底边),已知
 ,
,
 ,
,
 ,其中曲线
,其中曲线 是以
是以 为顶点、
为顶点、 为对称轴的抛物线的一部分.
为对称轴的抛物线的一部分.
(1)以 为原点,
为原点, 所在直线为
所在直线为 轴建立直角坐标系,求曲线
轴建立直角坐标系,求曲线 所在抛物线的方程;
所在抛物线的方程;
(2)求该公园的最大面积.
某风景区在一个直径AB为100米的半圆形花园中设计一条观光线路(如图所示).在点A与圆弧上的一点C之间设计为直线段小路,在路的两侧边缘种植绿化带;从点C到点B设计为沿弧BC的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
(Ⅰ)设 (弧度),将绿化带总长度表示为
(弧度),将绿化带总长度表示为 的函数
的函数 ;
;
(Ⅱ)试确定 的值,使得绿化带总长度最大.
的值,使得绿化带总长度最大.
在直角坐标系xOy中,曲线C1的参数方程为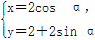 (α为参数).M是C1上的动点,P点满足
(α为参数).M是C1上的动点,P点满足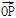 =2
=2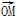 ,P点的轨迹为曲线C2.
,P点的轨迹为曲线C2.
(1)求C2的方程;
(2)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线θ= 与C1的异于极点的交点为A,与C2的异于极点的交点为B,求|AB|.
与C1的异于极点的交点为A,与C2的异于极点的交点为B,求|AB|.
已知函数 ,
, .
.
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求证:
时,求证: 在
在 上为增函数;
上为增函数;
(Ⅲ)若 在区间
在区间 上有且只有一个极值点,求
上有且只有一个极值点,求 的取值范围.
的取值范围.
已知椭圆 ,F为椭圆的右焦点,点A,B分别为椭圆的上下顶点,过点B作AF的垂线,垂足为M.
,F为椭圆的右焦点,点A,B分别为椭圆的上下顶点,过点B作AF的垂线,垂足为M.
(1)若 ,
, 的面积为1,求椭圆方程;
的面积为1,求椭圆方程;
(2)是否存在椭圆,使得点B关于直线AF对称的点D仍在椭圆上,若存在,求椭圆的离心率的值;若不存在,说明理由.
已知中心在坐标原点,焦点在 轴上的椭圆过点
轴上的椭圆过点 ,且它的离心率
,且它的离心率 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)与圆 相切的直线
相切的直线 交椭圆于
交椭圆于 两点,若椭圆上一点
两点,若椭圆上一点 满足
满足 ,求实数
,求实数 的取值范围.
的取值范围.
已知离心率为 的椭圆
的椭圆 的右焦点
的右焦点 是圆
是圆 的圆心,过椭圆上的动点
的圆心,过椭圆上的动点 作圆的两条切线分别交
作圆的两条切线分别交 轴于
轴于 (与
(与 点不重合)两点.
点不重合)两点.
(Ⅰ)求椭圆方程;
(Ⅱ)求线段 长的最大值,并求此时点
长的最大值,并求此时点 的坐标.
的坐标.
(本题满分16分,第1小题满分4分,第2小题满分6分,第3小题满分6分.)
已知椭圆
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,点
,点 是椭圆的一个顶点,△
是椭圆的一个顶点,△ 是等腰直角三角形.
是等腰直角三角形.
(1)求椭圆 的方程;
的方程;
(2)设点 是椭圆
是椭圆 上一动点,求线段
上一动点,求线段 的中点
的中点 的轨迹方程;
的轨迹方程;
(3)过点 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于 ,
, 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为 ,
, ,
,
且 ,探究:直线
,探究:直线 是否过定点,并说明理由.
是否过定点,并说明理由.