椭圆 的中心为坐标原点
的中心为坐标原点 ,焦点在
,焦点在 轴上,短轴长为
轴上,短轴长为 、离心率为
、离心率为 ,直线
,直线 与
与 轴交于点
轴交于点 ,与椭圆
,与椭圆 交于相异两点
交于相异两点 、
、 ,且
,且 .
.
(Ⅰ)求椭圆方程;(Ⅱ)求 的取值范围.
的取值范围.
设甲、乙、丙三个乒乓球协会的运动员人数分别为27,9,18,先采用分层抽样的方法从这三个协会中抽取6名运动员参加比赛.
(Ⅰ)求应从这三个协会中分别抽取的运动员人数;
(Ⅱ)将抽取的6名运动员进行编号,编号分别为 ,从这6名运动员中随机抽取2名参加双打比赛.
,从这6名运动员中随机抽取2名参加双打比赛.
(ⅰ)用所给编号列出所有可能的结果;
(ⅱ)设 为事件“编号为
为事件“编号为 的两名运动员至少有一人被抽到”,求事件
的两名运动员至少有一人被抽到”,求事件 发生的概率.
发生的概率.
已知点 在椭圆
在椭圆 上,如果经过点
上,如果经过点 的直线与椭圆只有一个公共点时,称直线为椭圆的切线,此时点
的直线与椭圆只有一个公共点时,称直线为椭圆的切线,此时点 称为切点,这条切线方程可以表示为:
称为切点,这条切线方程可以表示为: .根据以上性质,解决以下问题:
.根据以上性质,解决以下问题:
已知椭圆 ,若
,若 是椭圆
是椭圆 外一点(其中
外一点(其中 为定值),经过
为定值),经过 点作椭圆
点作椭圆 的两条切线,切点分别为
的两条切线,切点分别为 、
、 ,则直线
,则直线 的方程是______.
的方程是______.
已知椭圆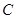 :
: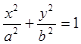 (
(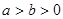 )的离心率
)的离心率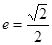 ,且过点
,且过点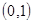 .
.
(1)求椭圆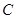 的方程;
的方程;
(2)如果直线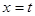 (
(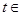 R)与椭圆相交于
R)与椭圆相交于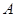 、
、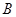 ,若
,若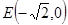 ,
, 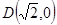 ,求证:直线
,求证:直线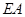 与直线
与直线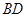 的交点
的交点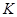 必在一条确定的双曲线上;
必在一条确定的双曲线上;
(3)若直线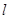 经过椭圆
经过椭圆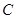 的左焦点交椭圆
的左焦点交椭圆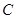 于
于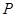 、
、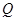 两点,
两点, 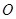 为坐标原点,且
为坐标原点,且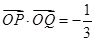 ,求直线
,求直线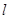 的方程.
的方程.
已知函数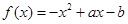
(1)若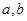 分别表示甲、乙两人各掷一次骰子所得的点数,求f(x)=0有解的概率;
分别表示甲、乙两人各掷一次骰子所得的点数,求f(x)=0有解的概率;
(2)若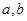 都是从区间[0,4]任取的一个实数,求f (1)>0成立的概率。
都是从区间[0,4]任取的一个实数,求f (1)>0成立的概率。