函数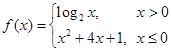 ,若实数
,若实数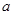 满足
满足 =1,则实数
=1,则实数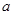 的所有取值的和为( )
的所有取值的和为( )
| A.1 | B. |
C. |
D.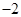 |
已知函数 是
是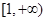 上的增函数.当实数
上的增函数.当实数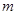 取最大值时,若存在点
取最大值时,若存在点 ,使得过点
,使得过点 的直线与曲线
的直线与曲线 围成两个封闭图形,且这两个封闭图形的面积总相等,则点
围成两个封闭图形,且这两个封闭图形的面积总相等,则点 的坐标为( )
的坐标为( )
A. |
B. |
C. |
D. |
设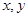 满足不等式组
满足不等式组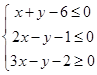 ,若
,若 的最大值为
的最大值为 ,最小值为
,最小值为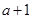 ,则实数
,则实数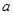 的取值范围为( )
的取值范围为( )
A. |
B. |
C.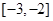 |
D. |
已知函数 的导数
的导数 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 .
.
(1)求b,c的值;
(2)求函数 的单调区间;
的单调区间;
(3)设函数 ,且
,且 在区间
在区间 内存在单调递减区间,求实数a的取值范围.
内存在单调递减区间,求实数a的取值范围.
如图,已知 平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,
平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形, ,
, ,
, ,
, .
.
(1)求证: 平面BCE;
平面BCE;
(2)求证: 平面BCE;
平面BCE;
(3)求三棱锥 的体积.
的体积.
已知函数 ,
, ,(
,( 为自然对数的底数).
为自然对数的底数).
(1)若不等式 对于一切
对于一切 恒成立,求a的最小值;
恒成立,求a的最小值;
(2)若对任意的 ,在
,在 上总存在两个不同的
上总存在两个不同的
 ,使
,使 成立,求a的取值范围.
成立,求a的取值范围.
已知函数 的定义域为[2,3],值域为[1,4];设
的定义域为[2,3],值域为[1,4];设 .
.
(1)求a,b的值;
(2)若不等式 在
在 上恒成立,求实数k的取值范围;
上恒成立,求实数k的取值范围;
(3)若 有三个不同的实数解,求实数k的取值范围.
有三个不同的实数解,求实数k的取值范围.
已知函数 .
.
(1)当 ,存在
,存在 (
( 为自然对数的底数),使
为自然对数的底数),使 ,求实数
,求实数 的取值范围;
的取值范围;
(2)当 时,设
时,设 ,在
,在 的图象上是否存在不同的两点
的图象上是否存在不同的两点 ,使得
,使得 ?请说明理由.
?请说明理由.
已知抛物线 与圆
与圆 的两个交点之间的距离为4.
的两个交点之间的距离为4.
(1)求 的值;
的值;
(2)设过抛物线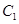 的焦点
的焦点 且斜率为
且斜率为 的直线与抛物线交于
的直线与抛物线交于 两点,与圆
两点,与圆 交于
交于 两点,当
两点,当 时,求
时,求 的取值范围.
的取值范围.