已知正四棱柱 中,
中, .
.
(Ⅰ)求证: ;
;
(Ⅱ)求钝二面角 的余弦值;
的余弦值;
(Ⅲ)在线段 上是否存在点
上是否存在点 ,使得平面
,使得平面
 平面
平面 ,若存在,求出
,若存在,求出 的值;若不存在,
的值;若不存在,
请说明理由.
已知函数f(x)=x3+x-16.
(1)求满足斜率为4的曲线的切线方程;
(2)求曲线y=f(x)在点(2,-6)处的切线的方程;
(3)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程.
已知函数 ,
, .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,求证:
时,求证: 在
在 上为增函数;
上为增函数;
(3)若 在区间
在区间 上有且只有一个极值点,求
上有且只有一个极值点,求 的取值范围.
的取值范围.
某高校共有学生 人,其中男生
人,其中男生 人,女生
人,女生 人.为调查该校学生
人.为调查该校学生
每周平均体育运动时间的情况,采用分层抽样的方法,收集 位学生每周平均体育运动时间的样本数据(单位:小时).
位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这 个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:
个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为: ,
, ,
, ,
, ,
,
 .估计该校学生每周平均体育运动时间超过
.估计该校学生每周平均体育运动时间超过 小时的概率;
小时的概率;

(3)在样本数据中,有 位女生的每周平均体育运动时间超过
位女生的每周平均体育运动时间超过 小时,请完成每周平均体育运动时间与性别列联表,并判断是否有
小时,请完成每周平均体育运动时间与性别列联表,并判断是否有 %的把握认为“该校学生的每周平均体育运动时间与性别有关”.
%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
一盒子装有 只产品,其中有
只产品,其中有 只一等品,
只一等品, 只二等品.从中取产品两次,每次任取一只,作不放回抽样.设事件
只二等品.从中取产品两次,每次任取一只,作不放回抽样.设事件 为“第一次取到的是一等品”,事件
为“第一次取到的是一等品”,事件 为“第二次取到的是一等品”,则条件概率
为“第二次取到的是一等品”,则条件概率 .
.
一个射箭运动员在练习时只记射中 环和
环和 环的成绩,未击中
环的成绩,未击中 环或
环或 环就以
环就以 环记.该远动员在练习时击中
环记.该远动员在练习时击中 环的概率为
环的概率为 ,击中
,击中 环的概率为
环的概率为 ,既未击中
,既未击中 环也未击中
环也未击中 环的概率为
环的概率为 (
( ,
, ,
, ),如果已知该运动员一次射箭击中环数的期望为
),如果已知该运动员一次射箭击中环数的期望为 环,则当
环,则当 取最小值时,
取最小值时, 的值为( )
的值为( )
A. |
B. |
C. |
D. |
北京某大学为第十八届四中全会招募了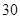 名志愿者(编号分别是
名志愿者(编号分别是 ,
,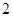 ,
, ,
,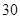 号),现从中任意选取
号),现从中任意选取 人按编号大小分成两组分配到江西厅、广电厅工作,其中三个编号较小的人在一组,三个编号较大的在另一组,那么确保
人按编号大小分成两组分配到江西厅、广电厅工作,其中三个编号较小的人在一组,三个编号较大的在另一组,那么确保 号、
号、 号与
号与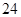 号同时入选并被分配到同一厅的选取种数是( )
号同时入选并被分配到同一厅的选取种数是( )
A.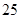 |
B.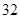 |
C.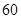 |
D.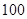 |
定圆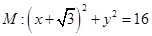 ,动圆
,动圆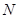 过点
过点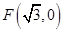 且与圆
且与圆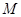 相切,记圆心
相切,记圆心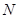 的轨迹为
的轨迹为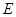 .
.
(1)求轨迹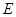 的方程;
的方程;
(2)设点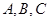 在
在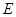 上运动,
上运动,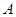 与
与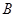 关于原点对称,且
关于原点对称,且 ,当
,当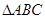 的面积最小时,求直线
的面积最小时,求直线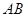 的方程.
的方程.