已知定义在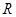 上的函数
上的函数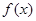 的图象是连续不断的,且有如下对应值表:
的图象是连续不断的,且有如下对应值表:
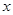 |
1 |
2 |
3 |
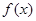 |
6.1 |
2.9 |
-3.5 |
那么函数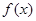 一定存在零点的区间是 ( )
一定存在零点的区间是 ( )
A.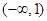 B.
B.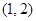 C.
C.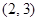 D.
D.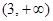
已知抛物线 的顶点在坐标原点
的顶点在坐标原点 ,对称轴为
,对称轴为 轴,焦点为
轴,焦点为 ,抛物线上一点
,抛物线上一点 的横坐标为
的横坐标为 ,且
,且 .
.
(1)求此抛物线 的方程;
的方程;
(2)过点 做直线
做直线 交抛物线
交抛物线 于
于 两点,求证:
两点,求证: .
.
已知函数 ,其中
,其中 且
且 .
.
(1)当 时,若
时,若 无解,求
无解,求 的范围;
的范围;
(2)若存在实数 ,
, (
( ),使得
),使得 时,函数
时,函数 的值域都也为
的值域都也为 ,求
,求 的范围.
的范围.
设数列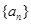 的前
的前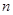 项和为
项和为 ,已知
,已知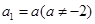 ,
,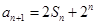 ,
, .
.
(1)设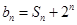 ,求证:数列
,求证:数列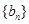 是等比数列;
是等比数列;
(2)若数列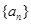 是单调递增数列,求实数
是单调递增数列,求实数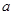 的取值范围.
的取值范围.
已知向量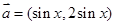 ,
,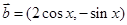 ,函数
,函数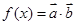 .
.
(1)求函数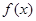 的最小正周期;
的最小正周期;
(2)求函数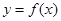 在
在 上的值域.
上的值域.
已知点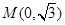 是椭圆
是椭圆 :
: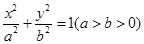 的一个顶点,椭圆
的一个顶点,椭圆 的离心率为
的离心率为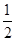 .
.
(1)求椭圆 的方程;
的方程;
(2)已知点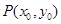 是定点,直线
是定点,直线 :
: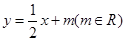 交椭圆
交椭圆 于不同的两点
于不同的两点 ,
, ,记直线
,记直线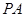 ,
,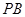 的斜率分别为
的斜率分别为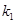 ,
,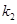 ,求点
,求点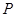 的坐标,使得
的坐标,使得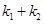 恒为0.
恒为0.
在四棱锥 中,
中, 平面
平面 ,底面
,底面 为直角梯形,
为直角梯形, ,
, ,且
,且 ,
, 分别为
分别为 ,
, 的中点.
的中点.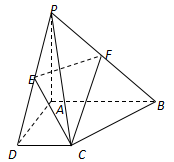
(1)求证: 平面
平面 ;
;
(2)若直线 与平面
与平面 的交点为
的交点为 ,且
,且 ,求截面
,求截面 与底面
与底面 所成锐二面角的大小.
所成锐二面角的大小.
如图, 是平面
是平面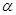 外固定的斜线段,
外固定的斜线段,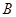 为斜足,若点
为斜足,若点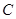 在平面
在平面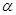 内运动,且
内运动,且 等于直线
等于直线 与平面
与平面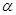 所成的角,则动点
所成的角,则动点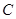 的轨迹为( )
的轨迹为( )
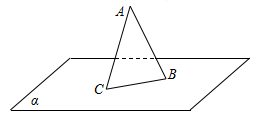
| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |