如图,在平面直角坐标系中,方程为 的圆
的圆 的内接四边形
的内接四边形 的对角线
的对角线 互相垂直,且
互相垂直,且 分别在
分别在 轴和
轴和 轴上.
轴上.
(1)若四边形 的面积为40,对角线
的面积为40,对角线 的长为8,
的长为8, ,且
,且 为锐角,求圆的方程,并求出
为锐角,求圆的方程,并求出 的坐标;
的坐标;
(2)设四边形 的一条边
的一条边 的中点为
的中点为 ,
, ,且垂足为
,且垂足为 ,试用平面解析几何的研究方法判断点
,试用平面解析几何的研究方法判断点 是否共线,并说明理由.
是否共线,并说明理由.
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的坐标分别对应数列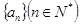 的前12项,如下表所示:
的前12项,如下表所示:

按如此规律下去,则 =___________________.
=___________________.
如图,AB是圆O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.
求证:(1) ;
;
(2)AB2=BE•BD-AE•AC.
某校从参加某次知识竞赛的同学中,选取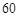 名同学将其成绩(百分制,均为整数)分成
名同学将其成绩(百分制,均为整数)分成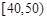 ,
,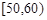 ,
,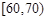 ,
,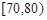 ,
,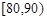 ,
,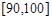 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题: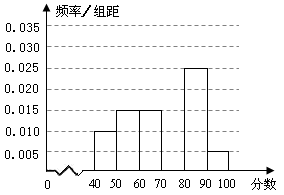
(1)求分数在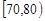 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的中位数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
有下列命题:
①在函数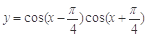 的图象中,相邻两个对称中心的距离为
的图象中,相邻两个对称中心的距离为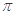 ;
;
②命题:“若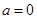 ,则
,则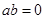 ”的否命题是“若
”的否命题是“若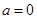 ,则
,则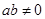 ”;
”;
③“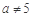 且
且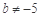 ”是“
”是“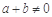 ”的必要不充分条件;
”的必要不充分条件;
④已知命题p:对任意的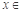 R,都有
R,都有 ,则
,则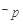 是:存在
是:存在 ,使得
,使得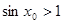 ;
;
⑤命题“若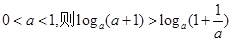 ”是真命题;
”是真命题;
⑥在△ABC中,若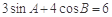 ,
,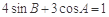 ,则角C等于
,则角C等于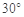 或
或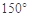 .
.
其中所有真命题的序号是 .
选修 :几何证明选讲
:几何证明选讲
如图,点 是⊙
是⊙ 直径
直径 的延长线上一点,
的延长线上一点, 是⊙
是⊙ 的切线,
的切线, 为切点,
为切点, 的平分线
的平分线 与
与 相交于点
相交于点 与
与 相交于点
相交于点

(1)求 的值;
的值;
(2)若 求
求 的值.
的值.
已知数列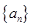 满足
满足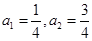 ,
, 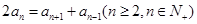 ,数列
,数列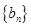 满足:
满足: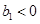 ,
,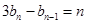
 ,数列
,数列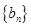 的前
的前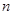 项和为
项和为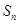 .
.
(1)求证:数列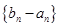 为等比数列;
为等比数列;
(2)求证:数列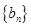 为递增数列;
为递增数列;
(3)若当且仅当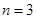 时,
时,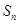 取得最小值,求
取得最小值,求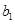 的取值范围.
的取值范围.