已知椭圆C: 的离心率为
的离心率为 ,以原点O为圆心,椭圆C的长半轴长为半径的圆与直线
,以原点O为圆心,椭圆C的长半轴长为半径的圆与直线 相切.
相切.
(1)求椭圆C的标准方程;
(2)已知点A,B为动直线 与椭圆C的两个交点,问:在
与椭圆C的两个交点,问:在 轴上是否存在定点E,使得
轴上是否存在定点E,使得 为定值?若存在,试求出点
为定值?若存在,试求出点 的坐标和定值;若不存在,请说明理由.
的坐标和定值;若不存在,请说明理由.
心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学 (男30女20), 给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
(1)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(2)经过多次测试后,甲每次解答一道几何题所用的时间在5—7分钟,乙每次解答一道几何题所用的时间在6—8分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
(3)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、 乙两女生被抽到的人数为X, 求X的分布列及数学期望E(X) .
附表及公式
选修4-4:极坐标系与参数方程
已知曲线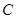 的参数方程为
的参数方程为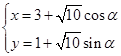 (
(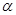 为参数),以直角坐标系原点为极点,
为参数),以直角坐标系原点为极点,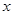 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线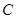 的极坐标方程,并说明其表示什么轨迹.
的极坐标方程,并说明其表示什么轨迹.
(2)若直线的极坐标方程为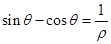 ,求直线被曲线
,求直线被曲线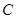 截得的弦长.
截得的弦长.
如图,圆 与
与 轴相切于点
轴相切于点 ,与
,与 轴正半轴相交于两点
轴正半轴相交于两点 (点
(点 在点
在点 的下方),且
的下方),且 .
.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)过点 任作一条直线与椭圆
任作一条直线与椭圆 相交于两点
相交于两点 ,连接
,连接 ,求证:
,求证: .
.
某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
| 年份x |
2011 |
2012 |
2013 |
2014 |
2015 |
| 储蓄存款y(千亿元) |
5 |
6 |
7 |
8 |
10 |
为了研究计算的方便,工作人员将上表的数据进行了处理,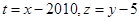 得到下表2:
得到下表2:
| 时间代号t |
1 |
2 |
3 |
4 |
5 |
| z |
0 |
1 |
2 |
3 |
5 |
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)通过(Ⅰ)中的方程,求出y关于x的回归方程;
(Ⅲ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程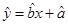 ,其中
,其中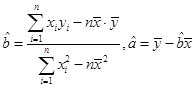 )
)