高中数学试题

已知直线（t为参数）．以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的坐标方程为．
（1）将曲线C的极坐标方程化为直坐标方程；
（2）设点M的直角坐标为，直线与曲线C的交点为A、B，求的值．

关于函数，看下面四个结论：
①是奇函数；
②当时，恒成立；
③的最大值是；
④的最小值是．
其中正确结论的个数为（    ）

A．1个

B．2个

C．3个

D．4个

若m是2和8的等比中项，则圆锥曲线的离心率是（   ）

A．

B．

C．或

D．或

如图所示，四边形ABCD为直角梯形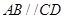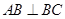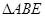，，，为等边三角形，且平面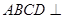平面ABE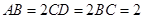，，P为CE中点．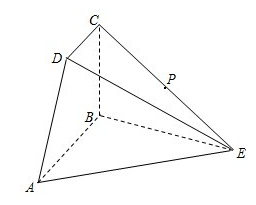

（1）求证：；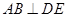
（2）求三棱锥D-ABP的体积．

已知函数f（x）=x²﹣lnx+x+1，g（x）=ae^x++ax﹣2a﹣1，其中a∈R．
（Ⅰ）若a=2，求f（x）的极值点；
（Ⅱ）试讨论f（x）的单调性；
（Ⅲ）若a＞0，∀x∈（0，+∞），恒有g（x）≥f′（x）（f′（x）为f（x）的导函数），求a的最小值．

已知抛物线C：x²=2py（p＞0）的焦点为F，抛物线上一点A的横坐标为x₁（x₁＞0），过点A作抛物线C的切线l₁交x轴于点D，交y轴于点Q，当|FD|=2时，∠AFD=60°．
（1）求证：FD垂直平分AQ，并求出抛物线C的方程；
（2）若B位于y轴左侧的抛物线C上，过点B作抛物线C的切线l₂交直线l₁于点P，AB交y轴于点（0，m），若∠APB为锐角，求m的取值范围．

已知椭圆C：的离心率为，其中左焦点（﹣2，0）．
（1）求椭圆C的方程；
（2）若直线y=x+m与椭圆C交于不同的两点A，B，求线段AB的最大值．

设定函数f（x）=x³+bx²+cx+d（a＞0），且方程f′（x）﹣9x=0的两个根分别为1，4．
（1）当a=3且曲线y=f（x）过原点时，求f（x）的解析式；
（2）若f（x）在（﹣∞，+∞）无极值点，求a的取值范围．

如图，已知六棱锥P﹣ABCDEF的底面是正六边形，PA⊥平面ABC，PA=2AB则下列结论正确的是（ ）

A．PB⊥AD

B．平面PAB⊥平面PBC

C．直线BC∥平面PAE

D．直线PD与平面ABC所成的角为45°

已知函数的导数为，且数列满足．
（1）若数列是等差数列，求的值；
（2）若对任意，都有，成立的取值范围．

分形是几何学是美籍法国数学家伯努瓦·曼德尔布罗（BenoitMandelbrot）在20世纪70年代创立的一门新学科，它的创立为解决传统科学众多领域的难题提供了全新的思路．按照下图1的分形规律可得到如图2所示的一个树形图，则当时，第行空心圆点个数与第行及第行空心圆点个数的关系式为________；第12行的实心圆点的个数是_______．

若满足条件，当且仅当时，取最小值，则实数的取值范围是（   ）

A．

B．

C．

D．

设函数，p为常数，．
（1）若对任意的，恒有，求p的取值范围；
（2）对任意的，函数恒成立，求实数a的取值范围．

已知函数，若函数有且仅有两个零点，则实数b的取值范围是（   ）

A．

B．

C．

D．

已知函数,函数
（1）当时，求时的最大值；
（2）若在恒成立，求的取值范围；
（3）当时，函数在有两个不同的零点，求的取值范围．