高中数学试题

已知是椭圆短轴上的两个端点，O为坐标原点，点A是椭圆长轴上的一个端点，点P是椭圆上异于的任意一点，点Q与点P关于轴对称，给出以下命题，其中所有正确命题的序号是            ．
①当P点的坐标为时，椭圆的离心率为；
②直线的斜率之积为定值；
③；
④的最大值为；
⑤直线的交点M在双曲线上．

如图，一圆形纸片的圆心为O，F是圆内一定点，M是圆周上一动点，把纸片折叠使点M与F重合，然后抹平纸片，折痕为CD，设CD与OM交于点P，则点P的轨迹是（  ）

A．双曲线	B．椭圆
C．抛物线	D．圆

如图，在正三棱柱ABC－A₁B₁C₁中，若AB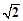＝BB₁，则AB₁与C₁B所成的角的大小为（  ）

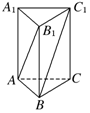
A．60°	B．90°
C．105°	D．75°

是方程表示椭圆的（  ）

A．充分不必要条件	B．必要不充分条件
C．充要条件	D．既不充分也不必要条件

已知双曲线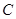的中心在坐标原点，焦点在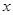轴上，离心率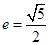，虚轴长为2．
（1）求双曲线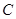的标准方程；
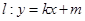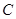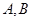（2）若直线与双曲线相交于两点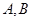，（均异于左、右顶点），且以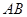为直径的圆过双曲线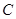的左顶点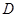，求证：直线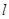过定点，并求出该定点的坐标．

在平面直角坐标系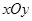中，已知椭圆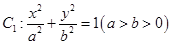的左焦点为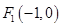，且椭圆上的点到焦点的距离的最小值为．
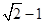（1）求椭圆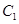的方程；
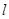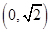（2）设直线过点且与椭圆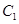相切，求直线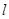的方程．

已知，若是的必要非充分条件，求实数的取值范围．

若命题“”是假命题，则实数的取值范围是            ．

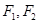如图，是双曲线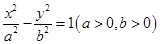的左、右焦点，过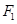的直线与双曲线的左右两支分别交于点．若为等边三角形，则双曲线的离心率为（  ）

A．4

B．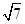

C．

D．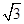

已知命题“若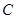，则”，命题的原命题，逆命题，否命题，逆否命题中真命题的个数为            ．

把圆与曲线的公共点用线段连接起来所得到的图形为（  ）

A．线段

B．不等边三角形

C．等边三角形

D．四边形

已知双曲线的中心在坐标原点，焦点在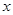轴上，离心率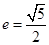，虚轴长为2．
（1）求双曲线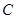的标准方程；
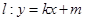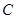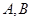（2）若直线与双曲线相交于两点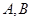，（均异于左、右顶点），且以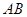为直径的圆过双曲线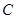的左顶点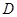，求证：直线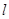过定点，并求出该定点的坐标．

已知动点与平面上两定点连线的斜率的积为定值-2．
（1）试求动点的轨迹方程；
（2）设直线与曲线交于两点，求．

已知函数且．当时，函数的零点，则          ．

已知椭圆，椭圆的右焦点为F．
（1）求过点F且斜率为1的直线被椭圆截得的弦长．
（2）求以M（1,1）为中点的椭圆的弦所在的直线方程．
（3）过椭圆的右焦点F的直线l交椭圆于A，B，求弦 AB的中点P的轨迹方程．