备战高频考点与最新模拟专题13统计
某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名.现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )
| A.6 | B.8 | C.10 | D.12 |
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高176cm的同学被抽中的概率.
在育民中学举行的电脑知识竞赛中,将高一两个班参赛学生的成绩(得分的整数)进行整理后分成五组,绘制出如下的频率分布直方图(如图),已知图中从左到右的第一、第二、第三、第四、第五小组的频率分别为0.30,0.15,0.10,0.05第二小组的频数为40.
(1)求第二小组的频率,并补全这个频率分布直方图;
(2)求这两个班参赛的学生人数.
北京市2013年4月1日-4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45.
(1)完成频率分布表;
(2)作出频率分布直方图;
(3)根据国家标准,污染指数在0~50之间时,空气质量为优;在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染.
请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
| 性别 是否需要志愿者 |
男 |
女 |
| 需要 |
40 |
30 |
| 不需要 |
160 |
270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由.

为了解某地区的中小学生视力情况,拟从该地区的中小学生中抽取部分学生进行调查,事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异,而男女生视力情况差异不大,在下面的抽样方法中,最合理的抽样方法是( )
| A.简单随机抽样 | B.按性别分层抽样 | C.按学段分层抽样 | D.系统抽样 |
某单位有840名职工, 现采用系统抽样方法, 抽取42人做问卷调查, 将840人按1, 2, …, 840随机编号, 则抽取的42人中, 编号落入区间[481, 720]的人数为 ( )
| A.11 | B.12 | C.13 | D.14 |
为了考察某校各班参加课外书法小组的人数,在全校随机抽取5个班级,把每个班级参加该小组的认为作为样本数据.已知样本平均数为7,样本方差为4,且样本数据互相不相同,则样本数据中的最大值为 .
某学校组织学生参加英语测试,成绩的频率分布直方图如图,
数据的分组一次为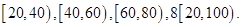
若低于60分的人数是15人,则该班的学生人数是
A.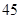 |
B. |
C. |
D. |
某学校有男、女学生各500名.为了解男女学生在学习兴趣与业余爱好方面是否存在显著差异,拟从全体学生中抽取100名学生进行调查,则宜采用的抽样方法是( )
| A.抽签法 | B.随机数法 | C.系统抽样法 | D.分层抽样法 |
某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是( )
| A.这种抽样方法是一种分层抽样 |
| B.这种抽样方法是一种系统抽样 |
| C.这五名男生成绩的方差大于这五名女生成绩的方差 |
| D.该班级男生成绩的平均数小于该班女生成绩的平均数 |
某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横的交叉点记忆三角形的顶点)处都种了一株相同品种的作物。根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示:
| X |
1 |
2 |
3 |
4 |
| Y |
51 |
48 |
45 |
42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米。
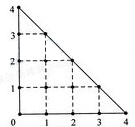
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)从所种作物中随机选取一株,求它的年收获量的分布列与数学期望。
某车间共有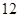 名工人,随机抽取
名工人,随机抽取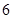 名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.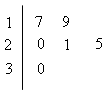
(1)根据茎叶图计算样本均值;
(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间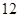 名工人中有几名优秀工人;
名工人中有几名优秀工人;
(3)从该车间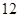 名工人中,任取
名工人中,任取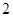 人,求恰有
人,求恰有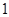 名优秀工人的概率.
名优秀工人的概率.
某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动,分别由李老师和张老师负责,已知该系共有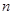 位学生,每次活动均需该系
位学生,每次活动均需该系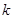 位学生参加(
位学生参加(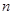 和
和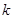 都是固定的正整数)。假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系
都是固定的正整数)。假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系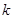 位学生,且所发信息都能收到。记该系收到李老师或张老师所发活动通知信息的学生人数为
位学生,且所发信息都能收到。记该系收到李老师或张老师所发活动通知信息的学生人数为
(1)求该系学生甲收到李老师或张老师所发活动通知信息的概率;
(2)求使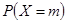 取得最大值的整数
取得最大值的整数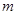 。
。
小波以游戏方式决定是参加学校合唱团还是参加学校排球队,游戏规则为:以0为起点,再从 ,
, (如图)这8个点中任取两点分别分终点得到两个向量,记这两个向量的数量积为X。若X=0就参加学校合唱团,否则就参加学校排球队。
(如图)这8个点中任取两点分别分终点得到两个向量,记这两个向量的数量积为X。若X=0就参加学校合唱团,否则就参加学校排球队。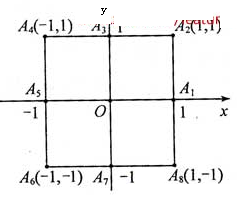
(1)求小波参加学校合唱团的概率;
(2)求X的分布列和数学期望.
现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(1)求张同学至少取到1道乙类题的概率;
(2)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是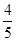 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用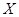 表示张同学答对题的个数,求
表示张同学答对题的个数,求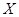 的分布列和数学期望.
的分布列和数学期望.
甲、乙两支排球队进行比赛,约定先胜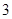 局者获得比赛的胜利,比赛随即结束。除第五局甲队获胜的概率是
局者获得比赛的胜利,比赛随即结束。除第五局甲队获胜的概率是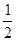 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是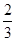 。假设各局比赛结果相互独立。
。假设各局比赛结果相互独立。
(1)分别求甲队以 胜利的概率;
胜利的概率;
(2)若比赛结果为求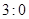 或
或 ,则胜利方得
,则胜利方得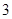 分,对方得
分,对方得 分;若比赛结果为
分;若比赛结果为 ,则胜利方得
,则胜利方得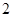 分、对方得
分、对方得 分。求乙队得分
分。求乙队得分 的分布列及数学期望。
的分布列及数学期望。
在一场娱乐晚会上, 有5位民间歌手(1至5号)登台演唱, 由现场数百名观众投票选出最受欢迎歌手.各位观众须彼此独立地在选票上选3名选手, 其中观众甲是1号歌手的歌迷, 他必选1号, 不选2号, 另在3至5号中随机选2名.观众乙和丙对5位歌手的演唱没有偏爱, 因此在1至5号中随机选3名歌手.
(1)求观众甲选中3号歌手且观众乙未选中3号歌手的概率;
(2)X表示3号歌手得到观众甲、乙、丙的票数之和, 求X的分布列和数学期望.
一个盒子里装有7张卡片, 其中有红色卡片4张, 编号分别为1, 2, 3, 4; 白色卡片3张, 编号分别为2, 3, 4.从盒子中任取4张卡片 (假设取到任何一张卡片的可能性相同).
(1)求取出的4张卡片中, 含有编号为3的卡片的概率.
(2)再取出的4张卡片中, 红色卡片编号的最大值设为X, 求随机变量X的分布列和数学期望.
设袋子中装有 个红球,
个红球, 个黄球,
个黄球, 个蓝球,且规定:取出一个红球得1分,
个蓝球,且规定:取出一个红球得1分,
取出一个黄球2分,取出蓝球得3分。
(1)当 时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量
时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量 为取出此2球所得分数之和,.求
为取出此2球所得分数之和,.求 分布列;
分布列;
(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量 为取出此球所得分数.若
为取出此球所得分数.若 ,求
,求
经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如右图所示。经销商为下一个销售季度购进了130t该农产品。以x(单位:t,100≤x≤150)表示下一个销售季度内经销该农产品的数量,T表示利润.
(1)将T表示为x的函数
(2)根据直方图估计利润T不少于57000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若x ,则取x=105,且x=105的概率等于需求量落入[100,110
,则取x=105,且x=105的概率等于需求量落入[100,110 ,求T的数学期望.
,求T的数学期望.
一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n。如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验。
假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为,且各件产品是否为优质品相互独立
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望。
以下命题中:①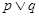 为假命题,则
为假命题,则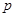 与
与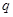 均为假命题
均为假命题
②对具有线性相关的变量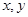 有一组观测数据
有一组观测数据 ,其回归直线方程是
,其回归直线方程是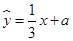 ,且
,且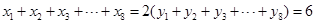 ,则实数
,则实数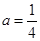
③对于分类变量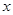 与
与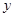 它们的随机变量
它们的随机变量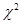 的观测值
的观测值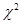 来说
来说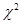 越小.“
越小.“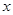 与
与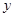 有关联”的把握程度越大
有关联”的把握程度越大
④已知 ,则函数
,则函数 的最小值为16.其中真命题的个数为 ( )
的最小值为16.其中真命题的个数为 ( )
| A.0 | B.1 | C.2 | D.3 |
某小卖部销售一品牌饮料的零售价x(元/评)与销售量y(瓶)的关系统计如下:
| 零售价x(元/瓶) |
3.0 |
3.2 |
3.4 |
3.6 |
3.8 |
4.0 |
| 销量y(瓶) |
50 |
44 |
43 |
40 |
35 |
28 |
已知的关系符合线性回归方程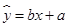 ,其中
,其中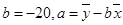 .当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
.当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
A.20 B.22 C.24 D.26
以下四个命题:
①从匀速传递的产品生产流水线上,质检员每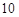 分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②若两个变量的线性相关性越强,则它们的相关系数的绝对值越接近于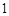 ;
;
③在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;
④对分类变量 与
与 的随机变量K2的观测值k来说,k越小,判断“
的随机变量K2的观测值k来说,k越小,判断“ 与
与 有关系”的把握越大.其中真命题的序号为( )
有关系”的把握越大.其中真命题的序号为( )
| A.①④ | B.②④ | C.①③ | D.②③ |
以下四个命题中:
①从匀速传递的产品生产流水线上,质检员每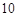 分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②若两个变量的线性相关性越强,则相关系数的绝对值越接近于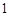 ;
;
③在某项测量中,测量结果 服从正态分布
服从正态分布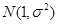
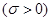 ,若
,若 位于区域
位于区域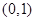 内的概率为
内的概率为 ,则
,则 位于区域
位于区域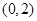 内的概率为
内的概率为 ;
;
④对分类变量 与
与 的随机变量K2的观测值k来说,k越小,判断“
的随机变量K2的观测值k来说,k越小,判断“ 与
与 有关系”的把握越大.其中真命题的序号为( )
有关系”的把握越大.其中真命题的序号为( )
| A.①④ | B.②④ | C.①③ | D.②③ |
从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为( )
| 分数 |
5 |
4 |
3 |
2 |
1 |
| 人数 |
20 |
10 |
30 |
30 |
10 |
A. B.3 C.
B.3 C. D.
D.
在某次测量中得到的 样本数据如下:
样本数据如下: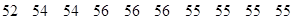 .若
.若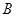 样本数据恰好是
样本数据恰好是 样本数据都加
样本数据都加 后所得数据,则
后所得数据,则 、
、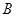 两样本的下列数字特征对应相同的是( )
两样本的下列数字特征对应相同的是( )
| A.众数 | B.平均数 | C.中位数 | D.标准差 |
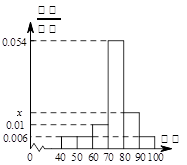
如图是某班50位学生期中考试数学成绩的频率分布直方图,其中成绩分组区间是: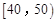 ,
,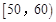 ,
,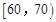 ,
, ,
,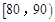 ,
, ,则图中
,则图中 的值等于 ( )
的值等于 ( )
A.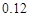 |
B.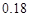 |
C.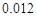 |
D.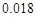 |
月底,某商场想通过抽取发票的10%来估计该月的销售额,先将该月的全部销售发票存根进行了编号:1,2,3,…,然后拟采用系统抽样的方法获取一个样本.若从编号为1,2,…,10的前10张发票存根中随机抽取一张,然后再按系统抽样的方法依编号逐次产生第二张、第三张、第四张、…,则抽样中产生的第二张已编号的发票存根,其编号不可能是( )
| A.19 | B.17 | C.23 | D.13 |
2014年3月,为了调查教师对第十二届全国人民代表大会第二次会议的了解程度,安庆市拟采用分层抽样的方法从 三所不同的中学抽取60教师进行调查。已知
三所不同的中学抽取60教师进行调查。已知 学校中分别有180、270、90名教师,则从
学校中分别有180、270、90名教师,则从 学校中应抽取的人数为( )
学校中应抽取的人数为( )
| A.10 | B.12 | C.18 | D.24 |
在演讲比赛决赛中,七位评委给甲、乙两位选手打分的茎叶图如图所示,但其中在 数据丢失。按照规则,甲、乙各去掉一个最高分和一个最低分,用
数据丢失。按照规则,甲、乙各去掉一个最高分和一个最低分,用 和
和 分别表示甲、乙两位选手获得的平均分,则( )
分别表示甲、乙两位选手获得的平均分,则( )

A. |
B. |
C. |
D. 和 和 之间的大小关系无法确定 之间的大小关系无法确定 |
为了调查你们学校高中学生身高分布情况,假设你的同桌抽取的样本容量与你抽取的样本容量相同且抽样方法合理,则下列结论正确的是( )
| A.你与你的同桌的样本频率分布直方图一定相同 |
| B.你与你的同桌的样本平均数一定相同 |
| C.你与你的同桌的样本的标准差一定相同 |
| D.你与你的同桌被抽到的可能性一定相同 |
已知变量x,y之间具有线性相关关系,其回归方程为 =-3+bx,若
=-3+bx,若 则b的值为( )
则b的值为( )
| A.2 | B.1 | C.-2 | D.-1 |
某校从参加高三年级期末考试的学生中随机抽取60名学生,将其数学成绩分成六段:[40,50),[50,60), …[90,100),它的频率分布直方图如图所示,则该批学生中成绩不低于60分的人数为___________.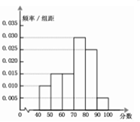
一个容量为20的样本数据分组后,分组与频数分别如下: ,2;
,2; ,3;
,3; ,4;
,4; ,5;
,5; ,4;
,4; ,2.则样本在
,2.则样本在 上的频率是 .
上的频率是 .
某校高三第一次模考中,对总分450分(含450分)以上的成绩进行统计,其频率分布直方图如图所示,若650~700分数段的人数为90,则500~550分数段的人数为_________人.
一支田径队有男女运动员98人,其中男运动员有56人.按男女比例用分层抽样的方法,从全体运动员中抽出一个容量为28的样本,那么应抽取女运动员人数是 .
给出下列命题:
① 已知线性回归方程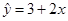 ,当变量
,当变量 增加2个单位,其预报值平均增加4个单位;
增加2个单位,其预报值平均增加4个单位;
② 在进制计算中, ;
;
③ 若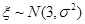 ,且
,且 ,则
,则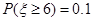 ;
;
④“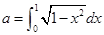 ”是“函数
”是“函数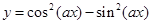 的最小正周期为4”的充要条件;
的最小正周期为4”的充要条件;
⑤ 设函数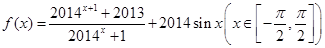 的最大值为M,最小值为m,则M+m=4027,其中正确命题的个数是 个。
的最大值为M,最小值为m,则M+m=4027,其中正确命题的个数是 个。
某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):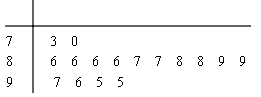
(1)指出这组数据的众数和中位数;
(2)若幸福指数不低于9.5分,则称该人的幸福指数为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记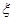 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求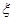 的分布列及数学期望.
的分布列及数学期望.
城市公交车的数量若太多则容易造成资源的浪费;若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示(单位:分钟):
| 组别 |
候车时间 |
人数 |
| 一 |
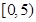 |
2 |
| 二 |
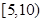 |
6 |
| 三 |
 |
4 |
| 四 |
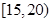 |
2 |
| 五 |
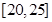 |
1 |
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中任选2人作进一步的调查,求抽到的两人恰好来自不同组的概率.
从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:
| 分组(重量) |
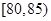 |
 |
 |
 |
| 频数(个) |
5 |
10 |
20 |
15 |
(1)根据频数分布表计算苹果的重量在 的频率;
的频率;
(2)用分层抽样的方法从重量在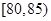 和
和 的苹果中共抽取4个,其中重量在
的苹果中共抽取4个,其中重量在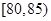 的有几个?
的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在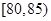 和
和 中各有1个的概率.
中各有1个的概率.
对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如下.
(1)求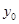 ,并根据图中的数据,用分层抽样的方法抽取
,并根据图中的数据,用分层抽样的方法抽取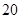 个元件,元件寿命落在
个元件,元件寿命落在 之间的应抽取几个?
之间的应抽取几个?
(2)从(1)中抽出的寿命落在 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个元件寿命落在
个元件,求事件“恰好有一个元件寿命落在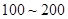 之间,一个元件寿命落在
之间,一个元件寿命落在 之间”的概率.
之间”的概率.
某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图.

(1)求分数在 的频率及全班人数;
的频率及全班人数;
(2)求分数在 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中 间矩形的高;
间矩形的高;
(3)若要从分数在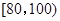 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在 之间的概率.
之间的概率.
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
|
5 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为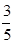 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)已知喜爱打篮球的10位女生中, 还喜欢打羽毛球,
还喜欢打羽毛球,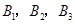 还喜欢打乒乓球,
还喜欢打乒乓球, 还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求
还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求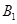 和
和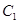 不全被选中的概率.
不全被选中的概率.
下面的临界值表供参考:
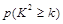 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: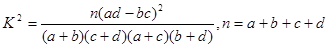 )
)
已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组.现要从中抽取10名学生,各组内抽取的编号按依次增加10进行系统抽样.
(1)若抽出的一个号码为22,则此号码所在的组数是多少?据此写出所有被抽出学生的号码;
(2)分别统计这10名学生的数学成绩,获得成绩数据的茎叶图如图4所示,求该样本的方差;
(3)在(2)的条件下,从这10名学生中随机抽取两名成绩不低于73分的学生,求被抽取到的两名学生的成绩之和不小于154分的概率.
随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是: ,2;
,2;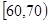 ,7;
,7;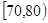 ,10;
,10; ,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.
,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.
(1)求样本的人数及x的值;
(2)估计样本的众数,并计算频率分布直方图中 的矩形的高;
的矩形的高;
(3)从成绩不低于80分的样本中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为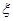 ,求
,求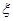 的数学期望.
的数学期望.
一汽车厂生产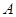 、
、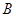 、
、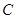 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)
| |
轿车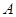 |
轿车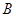 |
轿车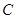 |
| 舒适型 |
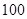 |
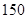 |
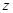 |
| 标准型 |
 |
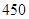 |
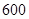 |
按类型分层抽样的方法在这个月生产的轿车中抽取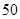 辆,其中有
辆,其中有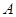 类轿车
类轿车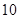 辆.
辆.
(1)求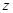 的值;
的值;
(2)用分层抽样的方法在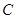 类轿车中抽取一个容量为
类轿车中抽取一个容量为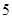 的样本.将该样本看成一个总体,从中任取
的样本.将该样本看成一个总体,从中任取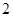 辆,求至少有
辆,求至少有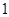 辆舒适型轿车的概率;
辆舒适型轿车的概率;
(3)用随机抽样的方法从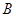 类舒适型轿车中抽取
类舒适型轿车中抽取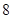 辆,经检测它们的得分如下:
辆,经检测它们的得分如下: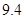 、
、 、
、 、
、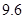 、
、 、
、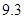 、
、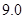 、
、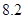 .把这
.把这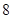 辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过
辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过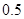 的概率
的概率
为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:

|
应该取消 |
应该保留 |
无所谓 |
||
| 在校学生 |
2100人 |
120人 |
y人 |
||
| 社会人士 |
600人 |
x人 |
z人 |
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.05.
(1)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.
大家知道,莫言是中国首位获得诺贝尔文学奖的文学家,国人欢欣鼓舞。某高校文学社从男女生中各抽取50名同学调查对莫言作品的了程度,结果如下:
(1)试估计该学校学生阅读莫言作品超过50篇的概率。
(2)对莫言作品阅读超过75篇的则称为“对莫言作品非常了解”,否则为“一般了解”,根据题意完成下表,并判断能否有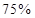 的把握认为对莫言作品的非常了解与性别有关?
的把握认为对莫言作品的非常了解与性别有关?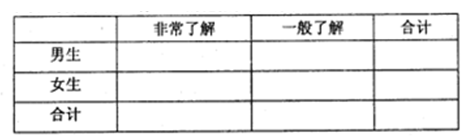

某中学举行了一次“环保知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
| 组别 |
分组 |
频数 |
频率 |
| 第1组 |
[50,60) |
8 |
0 16 |
| 第2组 |
[60,70) |
a |
▓ |
| 第3组 |
[70,80) |
20 |
0 40 |
| 第4组 |
[80,90) |
▓ |
0 08 |
| 第5组 |
[90,100] |
2 |
b |
| |
合计 |
▓ |
▓ |

(1)求出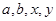 的值;
的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动
(ⅰ)求所抽取的2名同学中至少有1名同学来自第5组的概率;
(ⅱ)求所抽取的2名同学来自同一组的概率
 的公差,随机变量
的公差,随机变量 等可能地取值
等可能地取值
 的分布列为
的分布列为





 ( )
( ) B.
B. D.
D. 辆汽车通过某一段公路时的时速的频率分布直方图如下图所示,时速在
辆汽车通过某一段公路时的时速的频率分布直方图如下图所示,时速在 的汽车大约有______辆.
的汽车大约有______辆.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号