全国重点高中提前招生真题过关(十八)
已知 两点的坐标分别为 ,线段 上有一动点 ,过点 作 轴的平行线交抛物线 于 两点.若 ,则 的取值范围为( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在平面直角坐标系中,矩形 的顶点 在 轴的正半轴上,反比例函数 的图象经过顶点 ,分别与对角线 ,边 交于点 ,连接 .若点 为 的中点, 的面积为 ,则 的值为( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,从 的矩形 的较短边 上找一点 ,过这点剪下两个正方形,它们的边长分别是 ,当剪下的两个正方形的面积之和最小时,点 应选在( )

| A. |
的中点 |
B. |
|
| C. |
|
D. |
|
已知在 中, 是边 上的中点, 延长线上的点 满足 . 的内切圆与边 的切点分别为 ,延长 分别与 的延长线交于点 ,则 为( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 的半径为 ,圆心 的坐标为 ,点 是 上的任意一点, ,且 与 轴分别交于 两点,若点 ,点 关于原点 对称,则 的最小值为_____.

如图,在平面直角坐标系中,矩形 的两边 分别在坐标轴上,且 ,连接 .反比例函数 的图象经过线段 的中点 ,并与 分别交于点 .一次函数 的图象经过 两点.若点 是 轴上一动点,当 的值最小时,点 的坐标为_____.

将两个相似比为 的等腰直角三角形如图①放置,小直角三角形的斜边与大直角三角形的一直角边重合.绕点 旋转小直角三角形,使它的斜边与 交于点 的延长线与 交于点 ,如图②.若 ,则 _____.

小华用一张直角三角形纸片玩折纸游戏,如图①,在 中, .第一步,在 边上找一点 ,将纸片沿 折叠,点 落在 处,如图②;第二步,将纸片沿 折叠,点 落在 处,如图③.当点 恰好落在直角三角形纸片的边上时,线段 的长为_____.

设 为实数,且 ,拋物线 与 轴交于 两点,与 轴交于点 ,且抛物线的顶点在直线 上.若 是直角三角形,则 面积的最大值是_____.
已知平面直角坐标系中,点 和直线 (其中 不全为0 ,则点 到直线 的距离 可用公式 来计算.
例如:求点 到直线 的距离,因为直线 可化为 ,其中 ,所以点 到直线 的距离为 .根据以上材料,解答下列问题:
(1)求点 到直线 的距离;
(2)在(1)的条件下, 的半径 ,判断 与直线 的位置关系,若相交,设其弦长为 ,求 的值;若不相交,说明理由.
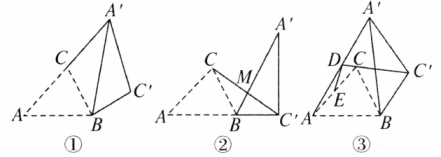
在Rt 中, ,将 绕点 顺时针旋转得到 ,其中点 的对应点分别为点 .
(1)如图①,当点 落在 的延长线上时,求 的长;
(2)如图②,当点 落在 的延长线上时,连接 交 于点 ,求 的长;
(3)如图③,连接 ,直线 交 于点 ,点 为 的中点,连接 .在旋转过程中, 是否存在最小值?若存在,求出 的最小值;若不存在,请说明理由.
两个水管同时开始向一个空容器内注水.如图是 两个水管各自的注水量 与注水时间 之间的函数图象,已知 水管的注水速度是 , 小时后, 水管的注水量随时间的变化是一段抛物线,其顶点是 ,且注水 小时,容器刚好注满.请根据图象所提供的信息解答下列问题:
(1)直接写出 注水量 与注水时间 之间的函数解解析式,并注明自变量的取值范围;
__________( ),
(2)求容器的容量;
(3)根据图象,通过计算回答,当 时,直接写出 的取值范围.

如图,点 是等边三角形 内一点,且 ,若将 绕着点 逆时针旋转后得到 .
(1)求点 与点 之间的距离;
(2)求 的度数.

如图,直线 与 轴交于点 ,与 轴交于点 ,抛物线 经过 两点.
(1)求抛物线的解析式;
(2)如图,点 是直线 上方抛物线上的一动点,当 面积最大时,请求出点 的坐标和 面积的最大值?



 粤公网安备 44130202000953号
粤公网安备 44130202000953号