如图,四边形 是菱形,点 为对角线 的中点,点 在 的延长线上, ,垂足为 ,点 在 的延长线上, ,垂足为 ,
(1)若 ,求证:四边形 是菱形;
(2)若 , 的面积为16,求菱形 的面积.

众志成城抗疫情,全国人民在行动.某公司决定安排大、小货车共20辆,运送260吨物资到 地和 地,支援当地抗击疫情.每辆大货车装15吨物资,每辆小货车装10吨物资,这20辆货车恰好装完这批物资.已知这两种货车的运费如下表:
目的地 车型 |
地(元 辆) |
地(元 辆) |
大货车 |
900 |
1000 |
小货车 |
500 |
700 |
现安排上述装好物资的20辆货车(每辆大货车装15吨物资,每辆小货车装10吨物资)中的10辆前往 地,其余前往 地,设前往 地的大货车有 辆,这20辆货车的总运费为 元.
(1)这20辆货车中,大货车、小货车各有多少辆?
(2)求 与 的函数解析式,并直接写出 的取值范围;
(3)若运往 地的物资不少于140吨,求总运费 的最小值.
如图, 为 的直径, 为 上一点, ,垂足为 , 平分 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.
甲、乙两个家庭来到以“生态资源,绿色旅游”为产业的美丽云南,各自随机选择到大理、丽江、西双版纳三个城市中的一个城市旅游.假设这两个家庭选择到哪个城市旅游不受任何因素影响,上述三个城市中的每一个被选到的可能性相同,甲、乙两个家庭选择到上述三个城市中的同一个城市旅游的概率为 .
(1)直接写出甲家庭选择到大理旅游的概率;
(2)用列表法或树状图法(树状图也称树形图)中的一种方法,求 的值.
某地响应“把绿水青山变成金山银山,用绿色杠杆撬动经济转型”发展理念,开展“美化绿色城市”活动,绿化升级改造了总面积为360万平方米的区域.实际施工中,由于采用了新技术,实际平均每年绿化升级改造的面积是原计划平均每年绿化升级改造的面积的2倍,所以比原计划提前4年完成了上述绿化升级改造任务.实际平均每年绿化升级改造的面积是多少万平方米?
某公司员工的月工资如下:
员工 |
经理 |
副经理 |
职员 |
职员 |
职员 |
职员 |
职员 |
职员 |
杂工 |
月工资 元 |
7000 |
4400 |
2400 |
2000 |
1900 |
1800 |
1800 |
1800 |
1200 |

经理、职员 、职员 从不同的角度描述了该公司员工的收入情况.
设该公司员工的月工资数据(见上述表格)的平均数、中位数、众数分别为 、 、 ,请根据上述信息完成下列问题:
(1) , , ;
(2)上月一个员工辞职了,从本月开始,停发该员工工资,若本月该公司剩下的8名员工的月工资不变,但这8名员工的月工资数据(单位:元)的平均数比原9名员工的月工资数据(见上述表格)的平均数减小了.你认为辞职的那名员工可能是 .
如图,两条抛物线 , 相交于 , 两点,点 在 轴负半轴上,且为抛物线 的最高点.
(1)求抛物线 的解析式和点 的坐标;
(2)点 是抛物线 上 , 之间的一点,过点 作 轴的垂线交 于点 ,当线段 取最大值时,求 .

[材料阅读]2020年5月27日,2020珠峰高程测量登山队成功登顶珠穆朗玛峰,将用中国科技“定义”世界新高度.其基本原理之一是三角高程测量法,在山顶上立一个觇标,找到2个以上测量点,分段测量山的高度,再进行累加.因为地球面并不是水平的,光线在空气中会发生折射,所以当两个测量点的水平距离大于 时,还要考虑球气差,球气差计算公式为 (其中 为两点间的水平距离, 为地球的半径, 取 ,即:山的海拔高度 测量点测得山的高度 测量点的海拔高度 球气差.
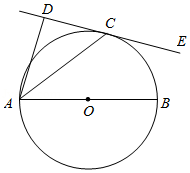
[问题解决]某校科技小组的同学参加了一项野外测量某座山的海拔高度活动.如图,点 , 的水平距离 ,测量仪 ,觇标 ,点 , , 在垂直于地面的一条直线上,在测量点 处用测量仪测得山顶觇标顶端 的仰角为 ,测量点 处的海拔高度为 .
(1)数据6400000用科学记数法表示为 ;
(2)请你计算该山的海拔高度.(要计算球气差,结果精确到
(参考数据: , ,
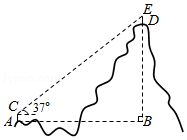
如图,点 是 的直径 延长线上的一点 ,点 是线段 的中点.
(1)尺规作图:在直径 上方的圆上作一点 ,使得 ,连接 , (保留清晰作图痕迹,不要求写作法);并证明 是 的切线;
(2)在(1)的条件下,若 , ,求 的长.

为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要 ;完成2间办公室和1间教室的药物喷洒要 .
(1)校医完成一间办公室和一间教室的药物喷洒各要多少时间?
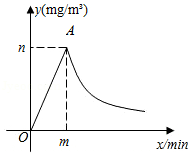
(2)消毒药物在一间教室内空气中的浓度 (单位: 与时间 (单位: 的函数关系如图所示:校医进行药物喷洒时 与 的函数关系式为 ,药物喷洒完成后 与 成反比例函数关系,两个函数图象的交点为 .当教室空气中的药物浓度不高于 时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.
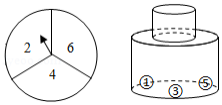
有一个可自由转动的转盘,被分成了三个大小相同的扇形,分别标有数字2,4,6;另有一个不透明的瓶子,装有分别标有数字1,3,5的三个完全相同的小球.小杰先转动一次转盘,停止后记下指针指向的数字(若指针指在分界线上则重转),小玉再从瓶子中随机取出一个小球,记下小球上的数字.
(1)请用列表或画树状图的方法(选其中一种)表示出所有可能出现的结果;
(2)若得到的两数字之和是3的倍数,则小杰贏;若得到的两数字之和是7的倍数,则小玉赢,此游戏公平吗?为什么?
某鞋店在一周内销售某款女鞋,尺码(单位: 数据收集如下:
24 |
23.5 |
21.5 |
23.5 |
24.5 |
23 |
22 |
23.5 |
23.5 |
23 |
22.5 |
23.5 |
23.5 |
22.5 |
24 |
24 |
22.5 |
25 |
23 |
23 |
23.5 |
23 |
22.5 |
23 |
23.5 |
23.5 |
23 |
24 |
22 |
22.5 |
绘制如图不完整的频数分布表及频数分布直方图:
尺码 |
划记 |
频数 |
|
|
3 |
|
|
|
|
|
13 |
|
|
2 |
(1)请补全频数分布表和频数分布直方图;
(2)若店主要进货,她最应该关注的是尺码的众数,上面数据的众数为 ;
(3)若店主下周对该款女鞋进货120双,尺码在 范围的鞋应购进约多少双?
