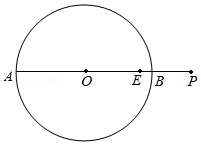
如图,点 是 的直径 延长线上的一点 ,点 是线段 的中点.
(1)尺规作图:在直径 上方的圆上作一点 ,使得 ,连接 , (保留清晰作图痕迹,不要求写作法);并证明 是 的切线;
(2)在(1)的条件下,若 , ,求 的长.
相关知识点
推荐套卷
如图,点 是 的直径 延长线上的一点 ,点 是线段 的中点.
(1)尺规作图:在直径 上方的圆上作一点 ,使得 ,连接 , (保留清晰作图痕迹,不要求写作法);并证明 是 的切线;
(2)在(1)的条件下,若 , ,求 的长.
