生活中，有人用纸条可以折成正五边形的形状，折叠过程是将图①中的纸条按图②方式拉紧，压平后可得到图③中的正五边形（阴影部分表示纸条的反面）．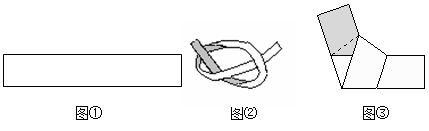
（1）将
两端剪掉则可以得到正五边形
，若将展开，展开后的平面图形是 ；
（2）若原长方形纸条（图①）宽为2cm，求（1）中展开后平面图形的周长（可以用三角函数表示）．
，其中
．
中，
，
是
的中点，连接
．
，
，
是垂足．图中共有多少对全等三角形？请直接用“
”符号把它们分别表示出来（不要求证明）．
相关知识点
推荐套卷
生活中，有人用纸条可以折成正五边形的形状，折叠过程是将图①中的纸条按图②方式拉紧，压平后可得到图③中的正五边形（阴影部分表示纸条的反面）．
（1）将两端剪掉则可以得到正五边形，若将展开，展开后的平面图形是 ；
（2）若原长方形纸条（图①）宽为2cm，求（1）中展开后平面图形的周长（可以用三角函数表示）．
粤公网安备 44130202000953号