已知:关于 的方程
的方程 有两个不相等的实数根.
有两个不相等的实数根.
(1)求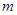 的取值范围;
的取值范围;
(2)抛物线 :
: 与
与 轴交于
轴交于 、
、 两点.若
两点.若 且直线
且直线 :
: 经过点
经过点 ,求抛物线
,求抛物线 的函数解析式;
的函数解析式;
(3)在(2)的条件下,直线 :
: 绕着点
绕着点 旋转得到直线
旋转得到直线 :
: ,设直线
,设直线 与
与 轴交于点
轴交于点 ,与抛物线
,与抛物线 交于点
交于点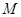 (
(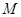 不与点
不与点 重合),当
重合),当 时,求
时,求 的取值范围.
的取值范围.
相关知识点
推荐套卷
已知:关于 的方程
的方程 有两个不相等的实数根.
有两个不相等的实数根.
(1)求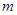 的取值范围;
的取值范围;
(2)抛物线 :
: 与
与 轴交于
轴交于 、
、 两点.若
两点.若 且直线
且直线 :
: 经过点
经过点 ,求抛物线
,求抛物线 的函数解析式;
的函数解析式;
(3)在(2)的条件下,直线 :
: 绕着点
绕着点 旋转得到直线
旋转得到直线 :
: ,设直线
,设直线 与
与 轴交于点
轴交于点 ,与抛物线
,与抛物线 交于点
交于点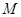 (
(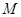 不与点
不与点 重合),当
重合),当 时,求
时,求 的取值范围.
的取值范围.