在全民健身运动中,骑行运动颇受市民青睐,甲、乙两骑行爱好者约定从A地沿相同路线骑行去距A地30千米的B地,已知甲骑行的速度是乙的1.2倍.
(1)若乙先骑行2千米,甲才开始从A地出发,则甲出发半小时恰好追上乙,求甲骑行的速度;
(2)若乙先骑行20分钟,甲才开始从A地出发,则甲、乙恰好同时到达B地,求甲骑行的速度.
已知一次函数 的图象与反比例函数 的图象相交于点 , .
(1)求一次函数的表达式,并在图中画出这个一次函数的图象;
(2)根据函数图象,直接写出不等式 的解集;
(3)若点C是点B关于y轴的对称点,连接AC,BC,求△ABC的面积.

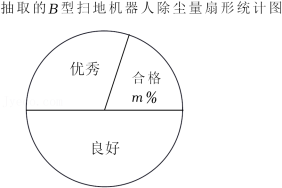
公司生产A、B两种型号的扫地机器人,为了解它们的扫地质量,工作人员从某月生产的A、B型扫地机器人中各随机抽取10台,在完全相同条件下试验,记录下它们的除尘量的数据(单位:g),并进行整理、描述和分析(除尘量用 表示,共分为三个等级:合格 ,良好 ,优秀 ),下面给出了部分信息:
10台A型扫地机器人的除尘量:83,84,84,88,89,89,95,95,95,98.
10台B型扫地机器人中“良好”等级包含的所有数据为:85,90,90,90,94
抽取的A、B型扫地机器人除尘量统计表
|
型号 |
平均数 |
中位数 |
众数 |
方差 |
“优秀”等级所占百分比 |
|
A |
90 |
89 |
a |
26.6 |
40% |
|
B |
90 |
b |
90 |
30 |
30% |
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,m= ;
(2)这个月公司可生产B型扫地机器人共3000台,估计该月B型扫地机器人“优秀”等级的台数;
(3)根据以上数据,你认为该公司生产的哪种型号的扫地机器人扫地质量更好?请说明理由(写出一条理由即可).
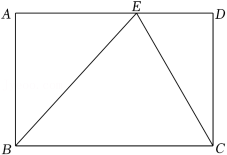
在学习矩形的过程中,小明遇到了一个问题:在矩形ABCD中,E是AD边上的一点,试说明△BCE的面积与矩形ABCD的面积之间的关系.他的思路是:首先过点E作BC的垂线,将其转化为证明三角形全等,然后根据全等三角形的面积相等使问题得到解决.请根据小明的思路完成下面的作图与填空:
证明:用直尺和圆规,过点E作BC的垂线EF,垂足为F(只保留作图痕迹).
在△BAE和△EFB中,
∵EF⊥BC,
∴∠EFB=90°.
又∠A=90°,
∴ ①
∵AD∥BC,
∴ ②
又 ③
∴△BAE≌△EFB(AAS).
同理可得 ④
∴ .
如图,在 中, , ,点 在 上, ,连接 , ,点 是边 上一动点(点 不与点 重合),过点 作 的垂线,与 相交于点 ,连接 ,设 , 与 重叠部分的面积为 .
(1)求 的长;
(2)求 关于 的函数解析式,并直接写出自变量 的取值范围.

是 的直径, 是 上一点, ,垂足为 ,过点 作 的切线,与 的延长线相交于点 .
(1)如图1,求证 ;
(2)如图2,连接 ,若 的半径为 , ,求 的长.

如图,莲花山是大连著名的景点之一.游客可以从山底乘坐索道车到达山顶,索道车运行的速度是 米/秒.小明要测量莲花山山顶白塔的高度,他在索道 处测得白塔底部 的仰角约为 ,测得白塔顶部 的仰角约为 ,索道车从 处运行到 处所用时间约为 分钟.
(1)索道车从 处运行到 处的距离约为_____米;
(2)请你利用小明测量的数据,求白塔BC的高度.(结果取整数)
(参考数据: , )

密闭容器内有一定质量的二氧化碳,当容器的体积 (单位: )变化时,气体的密度 (单位: )随之变化.已知密度 与体积 是反比例函数关系,它的图象如图所示,当 时, .
(1)求密度 关于体积V的函数解析式;
(2)若 ,求二氧化碳密度 的变化范围.

2022年北京冬奥会吉祥物冰墩墩和冬残奥会吉祥物雪容融深受大家喜爱.已知购买 个冰墩墩毛绒玩具和 个雪容融毛绒玩具用了 元,购买 个冰墩墩毛绒玩具和 个雪容融毛绒玩具用了 元.这两种毛绒玩具的单价各是多少元?
为了解某初级中学落实《中共中央国务院关于全面加强新时代大中小学劳动教育的意见》的实施情况,调查组从该校全体学生中随机抽取部分学生,调查他们平均每周劳动时间 (单位: ),并对数据进行整理、描述和分析.以下是根据调查结果绘制的统计图表的一部分.
平均每周劳动时间频数统计表
|
平均每周劳动时间 |
频数 |
频率 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
合计 |
|
根据以上信息,回答下列问题:
(1)填空: _____, _____, _____;
(2)若该校有 名学生,请估计平均每周劳动时间在 范围内的学生人数.

如图,在平面直角坐标系 中,抛物线 的顶点 在抛物线 上,直线 与抛物线 分别交于点 .
(1)求 的值;
(2)将 的纵坐标分别记为 ,设 ,若 的最大值为 ,则 的值是多少?
(3) 是 轴的正半轴上一点,且 的中点 恰好在抛物线 上.试探究:此时无论 为何负值,在 轴的负半轴上是否存在定点 ,使 总为直角?若存在,请求出点 的坐标;若不存在,请说明理由.

在某市组织的农机推广活动中,甲、乙两人分别操控A、B两种型号的收割机参加水稻收割比赛.已知乙每小时收割的亩数比甲少 ,两人各收割 亩水稻,乙则比甲多用 小时完成任务;甲、乙在收割过程中对应收稻谷有一定的遗落或破损,损失率分别为 .
(1)甲、乙两人操控A、B型号收割机每小时各能收割多少亩水稻?
(2)某水稻种植大户有与比赛中规格相同的 亩待收水稻,邀请甲、乙两人操控原收割机一同前去完成收割任务,要求平均损失率不超过 ,则最多安排甲收割多少小时?