已知两个二次函数 和 .对于函数 ,当 时,该函数取最小值.
(1)求 的值;
(2)若函数 的图象与坐标轴只有2个不同的公共点,求这两个公共点间的距离;
(3)若函数 、 的图象都经过点 ,过点 , 为实数)作 轴的平行线,与函数 、 的图象共有4个不同的交点,这4个交点的横坐标分别是 、 、 、 ,且 ,求 的最大值.
如图,在平面直角坐标系 中,将二次函数 的图象 沿 轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象 .
(1)求 的函数表达式;
(2)设点 是以点 为圆心、1为半径的圆上一动点,二次函数的图象 与 轴相交于两点 、 ,求 的最大值;
(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求 与 所围成封闭图形内(包括边界)整点的个数.

抛物线 经过点 ,顶点为 .
(1)求点 的坐标;
(2)设直线 与抛物线交于 、 两点(点 在点 的左侧).
①在抛物线的对称轴上是否存在点 .使 ?若存在,求出点 的坐标;若不存在,请说明理由;
②点 在直线 上,点 在抛物线上,当以 , , , 为顶点的四边形是平行四边形时,求点 的坐标.

如图,平面直角坐标系 中,点 ,函数 的图象经过 的顶点 和边 的中点 .
(1)求 的值;
(2)若 的面积等于6,求 的值;
(3)若 为函数 的图象上一个动点,过点 作直线 轴于点 ,直线 与 轴上方的 的一边交于点 ,设点 的横坐标为 ,当 时,求 的值.

如图,抛物线 的顶点为 ,该抛物线与 轴交于 、 两点,与 轴交于点 ,且 ,直线 与 轴交于点 .
(1)求抛物线的解析式;
(2)证明: ;
(3)在抛物线的对称轴上是否存在点 ,使 是等腰三角形?若存在,请直接写出符合条件的 点坐标,若不存在,请说明理由.

如图,抛物线 与 轴交于原点及点 ,且经过点 ,对称轴为直线 .
(1)求抛物线的解析式;
(2)设直线 与抛物线两交点的横坐标分别为 , ,当 时,求 的值;
(3)连接 ,点 为 轴下方抛物线上一动点,过点 作 的平行线交直线 于点 ,当 时,求出点 的坐标.
(坐标平面内两点 , , , 之间的距离
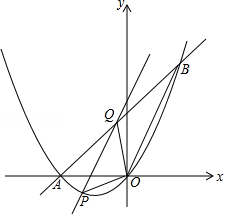
问题背景:
如图①,在四边形 中, , ,探究线段 , , 之间的数量关系.
小吴同学探究此问题的思路是:将 绕点 ,逆时针旋转 到 处,点 , 分别落在点 , 处(如图② ,易证点 , , 在同一条直线上,并且 是等腰直角三角形,所以 ,从而得出结论: .
简单应用:
(1)在图①中,若 , ,则 .
(2)如图③, 是 的直径,点 、 在 上, ,若 , ,求 的长.
拓展规律:
(3)如图④, , ,若 , ,求 的长(用含 , 的代数式表示)
(4)如图⑤, , ,点 为 的中点,若点 满足 , ,点 为 的中点,则线段 与 的数量关系是 .
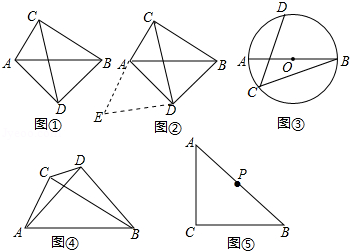
如图,正方形 的边长为1,点 在射线 上(异于点 、 ,直线 与对角线 及射线 分别交于点 、
(1)若 ,求 的度数;
(2)若点 在线段 上,过点 作 ,垂足为 ,当 时,求 的长;
(3)以 为直径作 .
①判断 和 的位置关系,并说明理由;
②当直线 与 相切时,直接写出 的长.
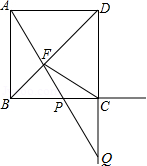
已知抛物线 过点 , 为抛物线的顶点.
(1)求抛物线的解析式;
(2)若点 、 均在抛物线上,其中点 ,且 ,求点 的坐标;
(3)如图,直线 与抛物线交于 、 两点.
①求证: ;
②求 面积的最小值.
如图,已知抛物线y=ax2+bx+c(a≠0)交x轴于A(﹣1,0),B(5,0)两点,与y轴交于点C(0,2)
(1)求抛物线的解析式;
(2)若点M为抛物线的顶点,连接BC、CM、BM,求△BCM的面积;
(3)连接AC,在x轴上是否存在点P使△ACP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
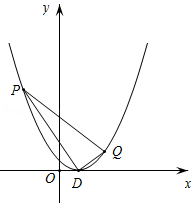
如图,直线y=- x+2与x轴交于点B,与y轴交于点C,已知二次函数的图象经过点B,C和点A(-1,0).
x+2与x轴交于点B,与y轴交于点C,已知二次函数的图象经过点B,C和点A(-1,0).
(1)求B,C两点坐标;
(2)求该二次函数的关系式;
(3)若抛物线的对称轴与x轴的交点为点D,点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标;
(4)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明问题.
如图,在直角坐标系 中,菱形 的边 在 轴正半轴上,点 , 在第一象限, ,边长 .点 从原点 出发沿 轴正半轴以每秒1个单位长的速度作匀速运动,点 从 出发沿边 以每秒2个单位长的速度作匀速运动,过点 作直线 垂直于 轴并交折线 于 ,交对角线 于 ,点 和点 同时出发,分别沿各自路线运动,点 运动到原点 时, 和 两点同时停止运动.
(1)当 时,求线段 的长;
(2)求 为何值时,点 与 重合;
(3)设 的面积为 ,求 与 的函数关系式及 的取值范围.

如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾斜度由45°降为30°,已知原滑滑板AB的长为5米,点D、B、C在同一水平地面上.求:改善后滑滑板会加长多少?(精确到0.01)(参考数据: =1.414,
=1.414, =1.732,
=1.732, =2.449)
=2.449)
某商场购进一批单价为4元的日用品.若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数y(件)与价格x(元/件)之间满足一次函数关系.
(1)试求y与x之间的函数关系式;
(2)当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?