甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为 ,羽毛球距地面高度 与其飞行的水平距离 之间的关系式为 .如图,已知球网 距原点 ,乙(用线段 表示)扣球的最大高度为 ,设乙的起跳点 的横坐标为 ,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则 的取值范围是( )

| A. |
|
B. |
|
| C. |
|
D. |
|
的三个顶点均在抛物线 上,并且斜边 轴,若斜边上的高为 ,则( )
| A. |
|
B. |
|
C. |
|
D. |
|
已知抛物线 的对称轴在 轴右侧,现将该抛物线先向右平移 个单位长度,再向上平移 个单位长度后,得到的抛物线正好经过坐标原点,则 的值是( )
| A. | 或 |
B. |
|
C. |
|
D. |
|
定义:我们将顶点的横坐标和纵坐标是互为相反数的二次函数称为“互异二次函数”.如图,在正方形 中,点 ,点 ,则“互异二次函数” 与正方形 有交点时 的最大值和最小值分别是( )

| A. |
|
B. |
|
C. |
|
D. |
|
已知二次函数 及一次函数 ,将该二次函数在 轴上方的图象沿 轴翻折到 轴下方,图象的其余部分不变,得到一个新函数(如图所示),请你在图中画出这个新图象,当直线 与新图象有 个交点时, 的取值范围是( )

| A. |
|
B. |
|
| C. |
|
D. |
|
四位同学在研究函数 是常数)时,甲发现当 时,函数有最小值;乙发现 是方程 的一个根;丙发现函数的最小值为3;丁发现当 时, ,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
| A. | 甲 |
B. | 乙 |
C. | 丙 |
D. | 丁 |
已知二次函数 ( 为常数),当自变量 的值满足 时,与其对应的函数值 的最大值为 ,则 的值为( )
| A. | 或 |
B. | 或 |
C. | 或 |
D. | 或 |
抛物线 与直线 围成的正方形有公共点,则实数 的取值范围是( )
| A. |
|
B. |
|
C. |
|
D. |
|
已知抛物线 是常数, 经过点 ,当 时,与其对应的函数值 .有下列结论:① ;②关于 的方程 有两个不等的实数根;③ .其中,正确结论的个数是( )
| A. |
|
B. |
|
C. |
|
D. |
|
已知二次函数 的图象如图所示,有下列 个结论:① ;② ;③ ;④ ;⑤若方程 有四个根,则这四个根的和为 .其中正确的结论有( )

| A. | 个 |
B. | 个 |
C. | 个 |
D. | 个 |
直线 过点 且与 轴垂直,若二次函数 (其中 是自变量)的图象与直线 有两个不同的交点,且其对称轴在 轴右侧,则 的取值范围是( )
| A. |
|
B. |
|
C. |
|
D. |
|
二次函数 的图象如图所示,有下列结论:① ;② ;③ ;④ ,正确的结论有( )

| A. | 个 |
B. | 个 |
C. | 个 |
D. | 个 |
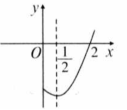
如图所示,已知抛物线 为常数, 经过点 ,且对称轴为直线 ,有下列结论:① ;② ;③ ;④无论 取何值,抛物线一定经过 ⑤ .其中正确的结论有( )
| A. | 个 |
B. | 个 |
C. | 个 |
D. | 个 |