已知:点D是等腰直角三角形ABC斜边BC所在直线上一点(不与点B重合),连接AD.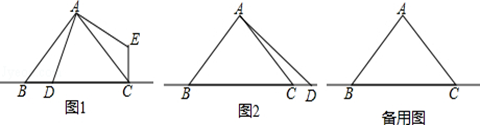
(1)如图1,当点D在线段BC上时,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.求证:BD=CE,BD⊥CE.
(2)如图2,当点D在线段BC延长线上时,探究AD、BD、CD三条线段之间的数量关系,写出结论并说明理由;
(3)若BD=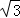 CD,直接写出∠BAD的度数.
CD,直接写出∠BAD的度数.
已知:直角梯形 中,
中,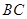 ∥
∥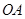 ,∠
,∠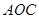 =
=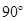 ,以
,以 为直径的圆
为直径的圆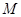 交
交 于点
于点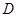 、
、 ,连结
,连结 、
、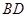 、
、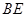 .
.
(1)在不添加其他字母和线的前提下,直接写出图1中的两对相似三角形:
_____________________,______________________ ;
(2)直角梯形 中,以
中,以 为坐标原点,
为坐标原点,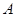 在
在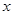 轴正半轴上建立直角坐标系(如图2),若抛物线
轴正半轴上建立直角坐标系(如图2),若抛物线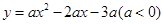 经过点
经过点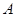 、
、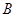 、
、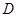 ,且
,且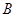 为抛物线的顶点.
为抛物线的顶点.
①写出顶点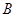 的坐标(用含
的坐标(用含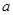 的代数式表示)___________;
的代数式表示)___________;
②求抛物线的解析式;
③在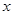 轴下方的抛物线上是否存在这样的点
轴下方的抛物线上是否存在这样的点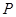 ,过点
,过点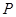 作
作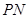 ⊥
⊥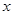 轴于点
轴于点 ,使得以点
,使得以点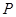 、
、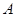 、
、 为顶点的三角形与△
为顶点的三角形与△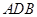 相似?
相似?
如图1,AB为⊙O的直径,点P是直径AB上任意一点,过点P作弦CD⊥AB,垂足为P,过点B的直线与线段AD的延长线交于点F,且∠F=∠ABC.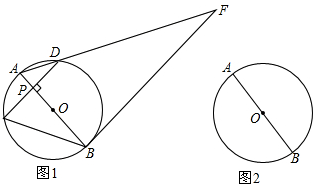
(1)若CD=2 ,BP=4,求⊙O的半径;
,BP=4,求⊙O的半径;
(2)求证:直线BF是⊙O的切线;
(3)当点P与点O重合时,过点A作⊙O的切线交线段BC的延长线于点E,在其它条件不变的情况下,判断四边形AEBF是什么特殊的四边形?请在图2中补全图象并证明你的结论.
如图1,在直角坐标系中,点A的坐标为(1,0),以OA为一边在第一象限内作正方形OABC,点D是x轴正半轴上一动点(OD>1,且OD≠2),连接BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交y轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.
(1)试找出图1中的一个损矩形 ;
(2)试说明(1)中找出的损矩形一定有外接圆;
(3)随着点D的位置变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由.
(4)在图2中,过点M作MG⊥y轴,垂足是点G,连结DN,若四边形DMGN为损矩形,求点D的坐标.
已知,如图,以点P(﹣1,0)为圆心的圆,交x轴于A、C两点(A在C的左侧),交y轴于B、D两点(B在D的上方),且∠BAC=30°,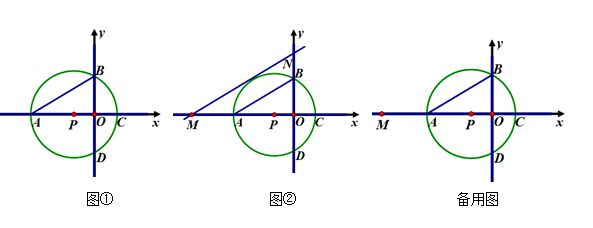
(1)如图①求⊙P的半径及点B的坐标;
(2)点Q是⊙P上任意一点,求△ABQ面积S的取值范围;
(3)如图②,已知点M(-5,0),过M作直线y=kx+b交y轴于点N,
①若MN//AB,试判断MN与⊙P的位置关系,并说明理由;
②在该直线上存在一点G,使以G、A、C为顶点的三角形是直角三角形,且满足条件的点G有且只有三个不同位置,求直线MN的函数关系式.
如图,△ABC内接于⊙O,AD⊥BC,OE⊥BC,OE= BC.
BC.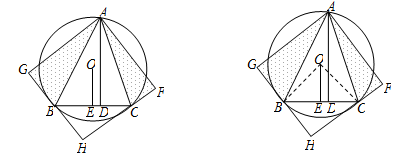
(1)求∠BAC的度数.
(2)将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.求证:四边形AFHG是正方形.
(3)若BD=6,CD=4,求AD的长.
如图,三角形ABC内接于圆O,AB=8,AC=6,D是AB边上的一点,P是优弧BAC的中点,连结PA,PB,PC,PD.
(1)当AD的长度为多少时三角形PAD是以AD为底边的等腰三角形?并证明.
(2)在(1)的条件下,若cos∠PCB= ,求PA的长.
,求PA的长.
如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,弧AE=弧 AB,BE分别交AD、AC于点F、G.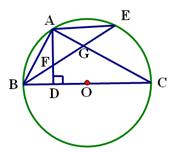
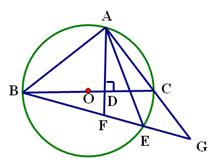
(1)判断△FAG的形状,并说明理由;
(2)若点E和点A在BC的两侧,BE、AC的延长线交于点G,AD的延长线交BE于点F,其余条件不变,(1)中的结论还成立吗?请说明理由.
如图,菱形ABCD的对角线AC、BD相交于点E,F是BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D、G两点,AD分别与EF,GF交于I、H两点.
(1)求证:AE∥FD;
(2)试判断AF和AB的数量关系,并证明你的结论;
(3)当G为线段DC的中点时,
①求证:AE=IE;
②设AC=12,BC=10,求GF的长.
如图,正方形ABCD的边长为4cm,点E、F在边AD上运动,且AE=DF.CF交BD于G,BE交AG于H.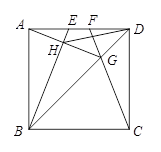
(1)求证:∠DAG=∠ABE;
(2)①求证:点H总在以AB为直径的圆弧上;
②画出点H所在的圆弧,并说明这个圆弧
的两个端点字母;
(3)直接写出线段DH长度的最小值.
如图,在菱形ABCD中,∠A=60°,以点D为圆心的⊙D与边AB相切于点E.
(1)求证:⊙D与边BC也相切;
(2)设⊙D与BD相交于点H,与边CD相交于点F,连接HF.若AB=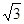 ,求图中阴影部分的面积(结果保留π);
,求图中阴影部分的面积(结果保留π);
(3)假设⊙D的半径为r,⊙D上一动点M从点F出发,按逆时针方向运动一周,当△MDF与△ABD的面积之比为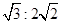 时,求动点M经过的弧长(结果用含r 的式子表示,保留π).
时,求动点M经过的弧长(结果用含r 的式子表示,保留π).
如图,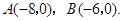 点
点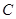 在
在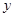 轴的正半轴上,
轴的正半轴上,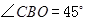 ,
,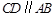 ,
,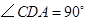 .点
.点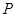 从点
从点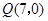 出发,沿
出发,沿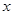 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为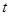 秒.
秒.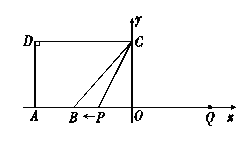
(1)点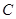 的坐标是 ;
的坐标是 ;
(2)当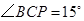 时,求
时,求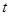 的值;
的值;
(3)以点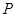 为圆心,
为圆心,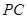 为半径的
为半径的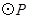 随点
随点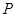 的运动而变化,当
的运动而变化,当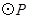 与四边形
与四边形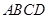 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求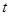 的值.
的值.
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长 AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题: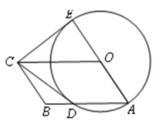
(1)求证:CD是⊙O的切线;
(2)若平行四边形OABC的两边长是方程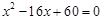 的两根,求平行四边形OABC的面积.
的两根,求平行四边形OABC的面积.
如图,在平面直角坐标系xOy中,⊙C经过点O,交x轴的正半轴于点B (2,0),P是 上的一个动点,且∠OPB=30°.设P点坐标为(m,n).
上的一个动点,且∠OPB=30°.设P点坐标为(m,n).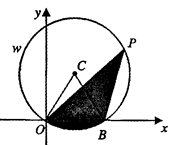
(1)当n=2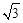 ,求m的值;
,求m的值;
(2)设图中阴影部分的面积为S,求S与n之间的函数关系式,并求S的最大值;
(3)试探索动点P在运动过程中,是否存在整点P(m,n)(横、纵坐标都为整数的点叫整点)?若存在,请求出;若不存在,请说明理由.