初中数学圆幂定理解答题

如图，点D是等边△ABC中BC边的延长线上一点，且AC=CD，以AB为直径作⊙O，分别交边AC、BC于点E、点F

（1）求证：AD是⊙O的切线；
（2）连接OC，交⊙O于点G，若AB=4，求线段CE、CG与围成的阴影部分的面积S．

如图，点C是半圆O的半径OB上的动点，作PC⊥AB于C．点D是半圆上位于PC左侧的点，连接BD交线段PC于E，且PD=PE．

（1）求证：PD是⊙O的切线；
（2）若⊙O的半径为4，PC=8，设OC=x，PD²=y．
①求y关于x的函数关系式；
②当x=时，求tanB的值．

如图，在△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作⊙O的切线，交AB于点E，交CA的延长线于点F．

（1）求证：FE⊥AB；
（2）当EF=6，时，求DE的长．

如图，在△ABC中，∠C=90°，AC+BC=8，点O是斜边AB上一点，以O为圆心的⊙O分别与AC，BC相切于点D，E．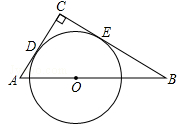

（1）当AC=2时，求⊙O的半径；
（2）设AC=x，⊙O的半径为y，求y与x的函数关系式．

如图，直线⊥线段于点，点在上，且，点是直线上的动点，作点关于直线的对称点，直线与直线相交于点，连接
（1）如图1，若点与点重合，则∠=    °，线段与的比值为    ；
（2）如图2，若点与点不重合，设过、、三点的圆与直线相交于，连接。求证：①=；②=2；
（3）如图3，，，则满足条件的点都在一个确定的圆上，在以下两小题中选做一题：
①如果你能发现这个确定圆的圆心和半径，那么不必写出发现过程，只要证明这个圆上的任意一点Q，都满足QA=2QB
②如果你不能发现这个确定圆的圆心和半径，那么请取几个特殊位置的点，如点在直线上、点与点重合等进行探究，求这个圆的半径

已知⊙O是以AB为直径的△ABC的外接圆，OD∥BC交⊙O于点D，交AC于点E，连接AD、BD，BD交AC于点F．

（1）求证：BD平分∠ABC；
（2）延长AC到点P，使PF=PB，求证：PB是⊙O的切线；
（3）如果AB=10，cos∠ABC=，求AD．

如图，点A、B、C分别是⊙O上的点，CD是⊙O的直径，P是CD延长线上的一点，AP=AC．

（1）若∠ABC=60°．求证：AP是⊙O的切线；
（2）若点B是弧CD的中点，AB交CD于点E，CD=4，求BE•AB的值．

如图，⊙O为△ABC的外接圆，BC为⊙O的直径，AE为⊙O的切线，过点B作BD⊥AE于D．

（1）求证：∠DBA=∠ABC；
（2）如果BD=1，tan∠BAD=，求⊙O的半径．

如图，已知点D在双曲线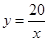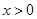（）的图象上，以D为圆心的⊙D与y轴相切于点C（0，4），与x轴交于A，B两点，抛物线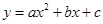经过A，B，C三点，点P是抛物线上的动点，且线段AP与BC所在直线有交点Q．

（1）写出点D的坐标并求出抛物线的解析式；
（2）证明∠ACO=∠OBC；
（3）探究是否存在点P，使点Q为线段AP的四等分点？若存在，求出点P的坐标；若不存在，请说明理由．

如图，在Rt△ABC中，∠C=90°，BE平分∠ABC交AC于点E，点D在AB上，DE⊥EB．

（1）求证：AC是△BDE的外接圆的切线；
（2）若AD=2，AE=6，求EC的长．

如图①、②，在平面直角坐标系中，点A的坐标为（4，0），以点A为圆心，4为半径的圆与轴于O，B两点，OC为弦，∠AOC=60°，P是轴上的一动点，连结CP．

（1）求的度数；
（2）如图①，当与⊙A相切时，求的长；
（3）如图②，当点在直径上时，的延长线与⊙A相交于点，问为何值时，是等腰三角形？

如图，PB为⊙O的切线，B为切点，过B作OP的垂线BA，垂足为C，交⊙O于点A，连接PA、AO，并延长AO交⊙O于点E，与PB的延长线交于点D．

（1）求证：PA是⊙O的切线；
（2）若，且OC=4，求PA的长和tanD的值．

如图，点在的直径的延长线上，点在上，，

（1）求证：CD是的切线；
（2）若的半径为3，求CD的长．

问题探究：
（一）新知学习：
圆内接四边形的判断定理：如果四边形对角互补，那么这个四边形内接于圆（即如果四边形EFGH的对角互补，那么四边形EFGH的四个顶点E、F、G、H都在同个圆上）．
（二）问题解决：
已知⊙O的半径为2，AB，CD是⊙O的直径．P是上任意一点，过点P分别作AB，CD的垂线，垂足分别为N，M．
（1）若直径AB⊥CD，对于上任意一点P（不与B、C重合）（如图一），证明四边形PMON内接于圆，并求此圆直径的长；
（2）若直径AB⊥CD，在点P（不与B、C重合）从B运动到C的过程汇总，证明MN的长为定值，并求其定值；
（3）若直径AB与CD相交成120°角．
①当点P运动到的中点P₁时（如图二），求MN的长；
②当点P（不与B、C重合）从B运动到C的过程中（如图三），证明MN的长为定值．
（4）试问当直径AB与CD相交成多少度角时，MN的长取最大值，并写出其最大值．

如图，已知AB是⊙O的直径，P为⊙O外一点，且OP∥BC，∠P=∠BAC．

（1）求证：PA为⊙O的切线；
（2）若OB=5，OP=，求AC的长．