如图①、②,在平面直角坐标系中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与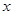 轴于O,B两点,OC为弦,∠AOC=60°,P是
轴于O,B两点,OC为弦,∠AOC=60°,P是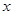 轴上的一动点,连结CP.
轴上的一动点,连结CP.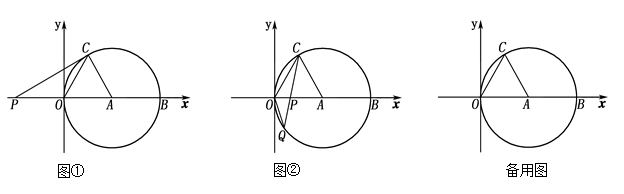
(1)求 的度数;
的度数;
(2)如图①,当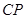 与⊙A相切时,求
与⊙A相切时,求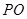 的长;
的长;
(3)如图②,当点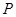 在直径
在直径 上时,
上时,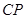 的延长线与⊙A相交于点
的延长线与⊙A相交于点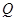 ,问
,问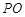 为何值时,
为何值时,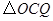 是等腰三角形?
是等腰三角形?
相关知识点
推荐套卷
如图①、②,在平面直角坐标系中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与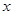 轴于O,B两点,OC为弦,∠AOC=60°,P是
轴于O,B两点,OC为弦,∠AOC=60°,P是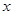 轴上的一动点,连结CP.
轴上的一动点,连结CP.
(1)求 的度数;
的度数;
(2)如图①,当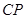 与⊙A相切时,求
与⊙A相切时,求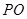 的长;
的长;
(3)如图②,当点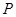 在直径
在直径 上时,
上时,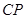 的延长线与⊙A相交于点
的延长线与⊙A相交于点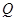 ,问
,问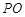 为何值时,
为何值时,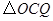 是等腰三角形?
是等腰三角形?