如图,点C的坐标为(0,3),点A的坐标为( ,0),点B在
,0),点B在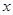 轴上方且BA⊥
轴上方且BA⊥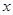 轴,
轴, ,过点C作CD⊥AB于D,点P是线段OA上一动点,PM∥AB交BC于点M,交CD于点Q,以PM为斜边向右作直角三角形PMN,∠MPN=
,过点C作CD⊥AB于D,点P是线段OA上一动点,PM∥AB交BC于点M,交CD于点Q,以PM为斜边向右作直角三角形PMN,∠MPN=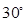 ,PN、MN的延长线交直线AB于E、F,设PO的长为
,PN、MN的延长线交直线AB于E、F,设PO的长为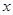 ,EF的长为
,EF的长为 .
.求线段PM的长(用
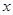 表示);
表示);求点N落在直线AB上时
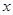 的值
的值求PE是线段MF的垂直平分线时直线PE的解析式;
求
 与
与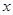 的函数关系式并写出相应的自变量
的函数关系式并写出相应的自变量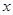 取值范围.
取值范围.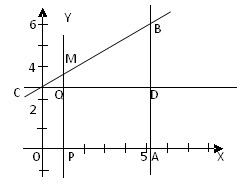

相关知识点
推荐套卷
 (2)、
(2)、 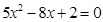

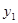 (单位:
(单位: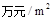 )与月份x(6≤x≤11,x为整数)之间满足一次函数关系,每月的销售面积为
)与月份x(6≤x≤11,x为整数)之间满足一次函数关系,每月的销售面积为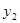 (单位:
(单位: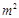 ),其中y2=-2000x+26000(6≤x≤11,x为整数).
),其中y2=-2000x+26000(6≤x≤11,x为整数).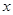 的函数关系式;
的函数关系式;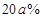 ,于是决定将12月份的销售价格在11月的基础上增加
,于是决定将12月份的销售价格在11月的基础上增加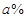 ,该计划顺利完成.为了尽快收回资金,2014年1月公司进行降价促销,该月销售额为(1500+600a)万元.这样12月、1月的销售额共为
,该计划顺利完成.为了尽快收回资金,2014年1月公司进行降价促销,该月销售额为(1500+600a)万元.这样12月、1月的销售额共为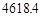 万元,请根据以上条件求出
万元,请根据以上条件求出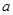 的值为多少?
的值为多少?
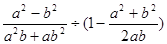 .其中
.其中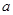 ,
,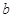 满足
满足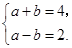
 粤公网安备 44130202000953号
粤公网安备 44130202000953号