已知,如图,以点P(﹣1,0)为圆心的圆,交x轴于A、C两点(A在C的左侧),交y轴于B、D两点(B在D的上方),且∠BAC=30°,
(1)如图①求⊙P的半径及点B的坐标;
(2)点Q是⊙P上任意一点,求△ABQ面积S的取值范围;
(3)如图②,已知点M(-5,0),过M作直线y=kx+b交y轴于点N,
①若MN//AB,试判断MN与⊙P的位置关系,并说明理由;
②在该直线上存在一点G,使以G、A、C为顶点的三角形是直角三角形,且满足条件的点G有且只有三个不同位置,求直线MN的函数关系式.
推荐套卷
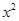 y﹣[2
y﹣[2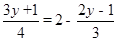 .
.
 DE;
DE; ,求DE的长.
,求DE的长. 粤公网安备 44130202000953号
粤公网安备 44130202000953号