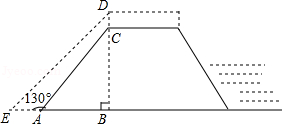
为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形 .已知迎水坡面 米,背水坡面 米, ,加固后拦水坝的横断面为梯形 , ,则 的长为 米.

如图, 某数学活动小组为测量学校旗杆 的高度, 沿旗杆正前方 米处的点 出发, 沿斜面坡度 的斜坡 前进 4 米到达点 ,在点 处安置测角仪, 测得旗杆顶部 的仰角为 ,量得仪器的高 为 1.5 米 . 已知 、 、 、 、 在同一平面内, , . 求旗杆 的高度 . (参 考数据: , , . 计算结果保留根号)

某体育看台侧面的示意图如图所示,观众区 的坡度 为 ,顶端 离水平地面 的高度为 ,从顶棚的 处看 处的仰角 ,竖直的立杆上 、 两点间的距离为 , 处到观众区底端 处的水平距离 为 .求:
(1)观众区的水平宽度 ;
(2)顶棚的 处离地面的高度 . , ,结果精确到

如图所示,某拦水大坝的横断面为梯形 , 、 为梯形的高,其中迎水坡 的坡角 ,坡长 米,背水坡 的坡度 为 与 的比值),则背水坡 的坡长为 米.

如图,信号塔 座落在坡度 的山坡上,其正前方直立着一警示牌.当太阳光线与水平线成 角时,测得信号塔 落在斜坡上的影子 长为 米,落在警示牌上的影子 长为3米,求信号塔 的高.(结果不取近似值)

为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即 米),背水坡 的坡度 (即 ,如图所示,已知 米, ,求水坝原来的高度 .
(参考数据: , ,
如图,为了测量山坡护坡石坝的坡度(坡面的铅直高度与水平宽度的比称为坡度),把一根长 的竹竿 斜靠在石坝旁,量出杆长 处的 点离地面的高度 ,又量得杆底与坝脚的距离 ,则石坝的坡度为

A. B.3C. D.4
某居民楼紧挨一座山坡 ,经过地质人员勘测,当坡度不超过 时,可以确保山体不滑坡,如图所示,已知 ,斜坡 的坡角 ,为防止滑坡,现对山坡进行改造,改造后,斜坡 与地面 成 角, 米.求斜坡 的长是多少米?(结果精确到0.1米,参考数据: ,

如图,这是一座一侧有缓步台的过街天桥示意图.已知桥面 长为 ,与水平面的垂直距离为 ,桥面 长为 ,与水平面的垂直距离为 .斜坡 , 与水平面的夹角分别为 , ,斜坡 的坡度(即 为 .求天桥跨度 的长.
参考数据: , ,

某地的一座人行天桥如图所示,天桥高为6米,坡面 的坡度为 ,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为 .
(1)求新坡面的坡角 ;
(2)原天桥底部正前方8米处( 的长)的文化墙 是否需要拆除?请说明理由.

如图,长 的楼梯 的倾斜角 为 ,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角 为 ,则调整后的楼梯 的长为

A. B. C. D.
如图, 是路边坡角为 ,长为10米的一道斜坡,在坡顶灯杆 的顶端 处有一探射灯,射出的边缘光线 和 与水平路面 所成的夹角 和 分别是 和 (图中的点 、 、 、 、 、 均在同一平面内, .
(1)求灯杆 的高度;
(2)求 的长度(结果精确到0.1米).(参考数据: . , ,

如图,小刚从山脚 出发,沿坡角为 的山坡向上走了300米到达 点,则小刚上升了
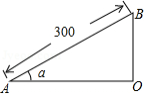
A. 米B. 米C. 米D. 米