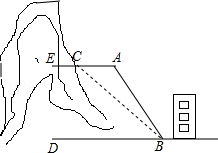
某居民楼紧挨一座山坡 ，经过地质人员勘测，当坡度不超过 时，可以确保山体不滑坡，如图所示，已知 ，斜坡 的坡角 ，为防止滑坡，现对山坡进行改造，改造后，斜坡 与地面 成 角， 米．求斜坡 的长是多少米？（结果精确到0.1米，参考数据： ，
相关试题
（本小题满分7分）
如图，小明站在A处放风筝，风筝飞到C处时的线长为20米，这时测得∠CBD=60°，若牵引底端AB离地面1．5米，求此时离地面高度．（计算结果精确到0．1米，
如图，抛物线y=x2+mx+（m﹣1）与x轴交于点A（x1，0），B（x2，0），x1＜x2，与y轴交于点C（0，c），且满足x12+x22+x1x2=7．
（1）求抛物线的解析式；
（2）在抛物线上能不能找到一点P，使∠POC=∠PCO？若能，请求出点P的坐标；若不能，请说明理由
山地自行车越来越受到中学生的喜爱，各种品牌相继投放市场，某车行经营的A型车去年销售总额为5万元，今年每辆销售价比去年降低400元，若卖出的数量相同，销售总额将比去年减少20%．
（1）今年A型车每辆售价多少元？（用列方程的方法解答）
（2）该车计划新进一批A型车和新款B型车共60辆，且B型车的进货数量不超过A型车数量的两倍，应如何进货才能使这批车获利最多？
A，B两种型号车的进货和销售价格如下表：
| A型车 |
B型车 |
|
| 进货价格（元） |
1100 |
1400 |
| 销售价格（元） |
今年的销售价格 |
2000 |
相交于A、B两点，A点的坐标为（1，2）
相关知识点
推荐套卷
粤公网安备 44130202000953号