为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形 为矩形, ,其坡度为 ,将步梯 改造为斜坡 ,其坡度为 ,求斜坡 的长度.(结果精确到0.01 ,参考数据: ,

为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度,他站在距离教学楼底部
处6米远的地面
处,测得宣传牌的底部
的仰角为
,同时测得教学楼窗户
处的仰角为
、
、
、
在同一直线上).然后,小明沿坡度
的斜坡从
走到
处,此时
正好与地面
平行.
(1)求点到直线
的距离(结果保留根号);
(2)若小明在处又测得宣传牌顶部
的仰角为
,求宣传牌的高度
(结果精确到0.1米,
,
.

自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图1所示的坡路进行改造.如图2所示,改造前的斜坡米,坡度为
;将斜坡
的高度
降低
米后,斜坡
改造为斜坡
,其坡度为
.求斜坡
的长.(结果保留根号)

汛期即将来临,为保证市民的生命和财产安全,市政府决定对一段长200米且横断面为梯形的大坝用土石进行加固.如图,加固前大坝背水坡坡面从至
共有30级阶梯,平均每级阶梯高
,斜坡
的坡度
;加固后,坝顶宽度增加2米,斜坡
的坡度
,问工程完工后,共需土石多少立方米?(计算土石方时忽略阶梯,结果保留根号)

如图, 是一垂直于水平面的建筑物,某同学从建筑物底端 出发,先沿水平方向向右行走20米到达点 ,再经过一段坡度(或坡比)为 、坡长为10米的斜坡 到达点 ,然后再沿水平方向向右行走40米到达点 , , , , 均在同一平面内).在 处测得建筑物顶端 的仰角为 ,则建筑物 的高度约为(参考数据: , ,

| A. |
21.7米 |
B. |
22.4米 |
C. |
27.4米 |
D. |
28.8米 |
如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部 点处测得旗杆顶端的仰角 ,升旗台底部到教学楼底部的距离 米,升旗台坡面 的坡度 ,坡长 米,若旗杆底部到坡面 的水平距离 米,则旗杆 的高度约为 (参考数据: , ,

| A. |
12.6米 |
B. |
13.1米 |
C. |
14.7米 |
D. |
16.3米 |
如图,小王在长江边某瞭望台 处,测得江面上的渔船 的俯角为 ,若 米, 米, 平行于江面 ,迎水坡 的坡度 ,坡长 米,则此时 的长约为 (参考数据: , , .
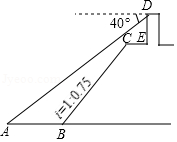
| A. |
5.1米 |
B. |
6.3米 |
C. |
7.1米 |
D. |
9.2米 |
如图所示,某办公大楼正前方有一根高度是15米的旗杆 ,从办公楼顶端 测得旗杆顶端 的俯角 是 ,旗杆底端 到大楼前梯坎底边的距离 是20米,梯坎坡长 是12米,梯坎坡度 ,则大楼 的高度约为 (精确到0.1米,参考数据: , ,

| A. |
30.6 |
B. |
32.1 |
C. |
37.9 |
D. |
39.4 |
如图,某商店营业大厅自动扶梯的倾斜角为
,
的长为12米,求大厅两层之间的距离
的长.(结果精确到0.1米)(参考数据:
,
,

如图,坡面CD的坡比为 ,坡顶的平地BC上有一棵小树AB,当 太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC="3" 米,斜坡上的树影CD=
,坡顶的平地BC上有一棵小树AB,当 太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC="3" 米,斜坡上的树影CD= 米,则小树AB的高是 .
米,则小树AB的高是 .

(年贵州省黔南州)如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i= :3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)