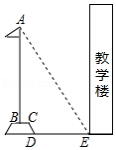
如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部 点处测得旗杆顶端的仰角 ,升旗台底部到教学楼底部的距离 米,升旗台坡面 的坡度 ,坡长 米,若旗杆底部到坡面 的水平距离 米,则旗杆 的高度约为 (参考数据: , ,
| A. |
12.6米 |
B. |
13.1米 |
C. |
14.7米 |
D. |
16.3米 |
相关知识点
推荐套卷
如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部 点处测得旗杆顶端的仰角 ,升旗台底部到教学楼底部的距离 米,升旗台坡面 的坡度 ,坡长 米,若旗杆底部到坡面 的水平距离 米,则旗杆 的高度约为 (参考数据: , ,

| A. |
12.6米 |
B. |
13.1米 |
C. |
14.7米 |
D. |
16.3米 |