如图,在 和 的斜边分别为正方形的边 和 ,其中 .
(1)求证: ;
(2)线段 与线段 相交于 ,若 ,求 的值.

已知在 中, , 为 的平分线,将 沿 所在的直线对折,使点 落在点 处,连接 , ,延长 交 于点 ,设 .
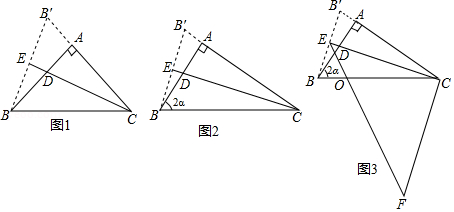
(1)如图1,若 ,求证: ;
(2)如图2,若 ,试求 与 的数量关系(用含 的式子表示);
(3)如图3,将(2)中的线段 绕点 逆时针旋转角 ,得到线段 ,连接 交 于点 ,设 的面积为 , 的面积为 ,求 (用含 的式子表示).
如图1,直线 与抛物线 相交于 、 两点,与 轴交于点 , 、 关于 轴对称,连接 、 .

(1)①求 、 的坐标;②求证: ;
(2)如图2,将题中直线 变为 ,抛物线 变为 ,其他条件不变,那么 是否仍然成立?请说明理由.
如图,在三角形 中, , ,以 为直径作 交 于点 ,交 于点 ,直线 是 的切线, 为切点,交 的延长线于点 .
(1)求证: ;
(2)求 的值.

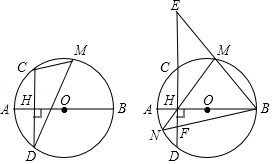
如图,已知 为 直径, 是 的中点, 交 的延长线于 , 的切线交 的延长线于 .
(1)求证:直线 与 相切;
(2)已知 且 , 的半径为5,求 的值.
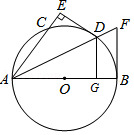
如图,已知在 中, ,以 为直径的 与 交于点 ,点 是 的中点,连接 , .
(1)若 ,求 ;
(2)求证: 是 的切线.
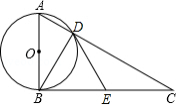
如图,已知四边形 内接于 , 是 的中点, 于 ,与 及 的延长线交于点 、 ,且 .
(1)求证: ;
(2)如果 , ,求 的值.

如图,以 的 边上一点 为圆心,经过 , 两点且与 边交于点 ,点 为 的下半圆弧的中点,连接 交线段 于点 ,若 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径 及 .

小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°-α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°-α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
如图,线段 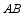 是
是 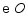 的直径,弦
的直径,弦 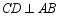 于点
于点 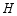 ,点
,点 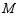 是
是 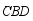 上任意一点,
上任意一点, 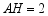 ,
, 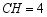 .
.
(1)求 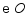 的半径
的半径 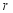 的长度;
的长度;
(2)求 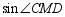 ;
;
(3)直线 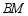 交直线
交直线 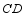 于点
于点 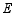 ,直线
,直线 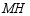 交
交 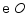 于点
于点 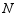 ,连接
,连接 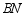 交
交 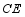 于点
于点 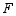 ,求
,求 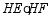 的值.
的值.
如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)
(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的 ,得到△A2B2C2,请在y轴右侧画出△A2B2C2,并求出∠A2C2B2的正弦值.

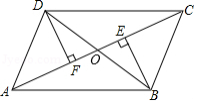
如图,在 中, 是对角线 、 的交点, , ,垂足分别为点 、 .
(1)求证: .
(2)若 , ,求 的值.
如图,二次函数的图象与
轴交于点
,过点
作
轴的平行线交抛物线于另一点
,抛物线过点
,且顶点为
,连接
、
、
、
.
(1)填空: ;
(2)点是抛物线上一点,点
的横坐标大于1,直线
交直线
于点
.若
,求点
的坐标;
(3)点在直线
上,点
关于直线
对称的点为
,点
关于直线
对称的点为
,连接
.当点
在
轴上时,直接写出
的长.

如图所示,的顶点
在正方形
对角线
的延长线上,
与
交于点
,连接
、
,满足
.
(1)求证:.
(2)若正方形的边长为1,
,求
的值.
