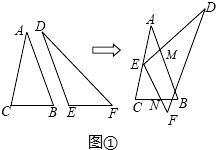
(年湖北江汉油田、潜江、天门、仙桃10分)如图①,△ABC与△DEF是将△ACF沿过A点的某条直线剪开得到的(AB,DE是同一条剪切线).平移△DEF使顶点E与AC的中点重合,再绕点E旋转△DEF,使ED,EF分别与AB,BC交于M,N两点.
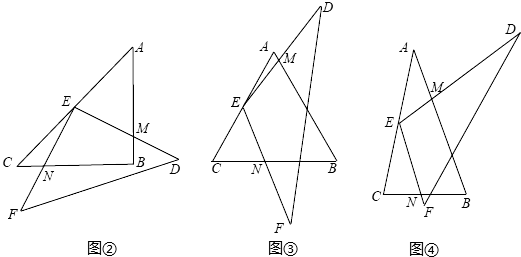
(1)如图②,△ABC中,若AB=BC,且∠ABC=90°,则线段EM与EN有何数量关系?请直接写出结论;
(2)如图③,△ABC中,若AB=BC,那么(1)中的结论是否还成立?若成立,请给出证明:若不成立,请说明理由;
(3)如图④,△ABC中,若AB:BC=m:n,探索线段EM与EN的数量关系,并证明你的结论.