如图, ,点 是 平分线上的一点,过点 分别作 , ,垂足分别为点 , , ,点 为线段 上的一点(点 不与点 、 重合),连接 ,以 为直角边,点 为直角顶点,作等腰直角三角形 ,点 落在 左侧.
(1)求证: ;
(2)连接 ,请你判断 与 的位置关系,并说明理由;
(3)设 , 的面积为 ,求 与 之间的函数关系式.

如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 ,过点 作 轴的垂线交直线 于点 ,过点 作 的垂线交 轴于点 ,此时点 与原点 重合,连接 交 轴于点 ,得到第1个△ ;过点 作 轴的垂线交 于点 ,过点 作 轴的平行线交 于点 ,连接 与 交于点 ,得到第2个△ 按照此规律进行下去,则第2019个△ 的面积是 .

如图,在△ 中, , ,过点 作 ,垂足为点 ,过点 作 交 于点 ,得到△ ;过点 作 ,垂足为点 ,过点 作 交 于点 ,得到△ ;过点 作 ,垂足为点 ,过点 作 交 于点 ,得到△ ; 按照上面的作法进行下去,则△ 的面积为 .(用含正整数 的代数式表示)

我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“内似线”.
(1)等边三角形“内似线”的条数为 ;
(2)如图, 中, ,点 在 上,且 ,求证: 是 的“内似线”;
(3)在 中, , , , 、 分别在边 、 上,且 是 的“内似线”,求 的长.

如图, 在矩形 中, , ,点 从点 出发, 沿对角线 向点 匀速运动, 速度为 ,过点 作 交 于点 ,以 为一边作正方形 ,使得点 落在射线 上, 点 从点 出发, 沿 向点 匀速运动, 速度为 ,以 为圆心, 为半径作 ,点 与点 同时出发, 设它们的运动时间为 (单 位: .
(1) 如图 1 ,连接 平分 时, 的值为 ;
(2) 如图 2 ,连接 ,若 是以 为底的等腰三角形, 求 的值;
(3) 请你继续进行探究, 并解答下列问题:
①证明: 在运动过程中, 点 始终在 所在直线的左侧;
②如图 3 ,在运动过程中, 当 与 相切时, 求 的值;并判断此时 与 是否也相切?说明理由 .
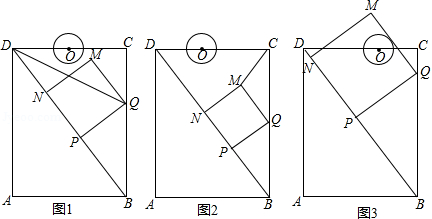
如图, 中, , , , 于点 , 是线段 上一点, , ,连接 、 .设 、 的中点分别为 、 .
(1)求 的长;
(2)求 的长;
(3)设 与 的交点为 ,请直接写出 的值.

阅读下面材料,完成(1) (3)题
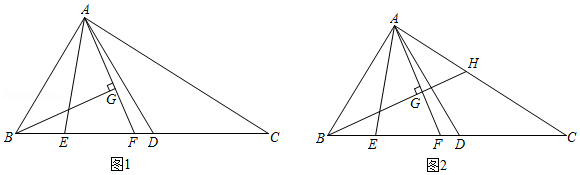
数学课上,老师出示了这样一道题:如图1, 中, ,点 、 在 上, , (其中 , 的平分线与 相交于点 , ,垂足为 ,探究线段 与 的数量关系,并证明.同学们经过思考后,交流了自己的想法:
小明:“通过观察和度量,发现 与 相等.”
小伟:“通过构造全等三角形,经过进一步推理,可以得到线段 与 的数量关系.”
老师:“保留原题条件,延长图1中的 ,与 相交于点 (如图 ,可以求出 的值.”
(1)求证: ;
(2)探究线段 与 的数量关系(用含 的代数式表示),并证明;
(3)直接写出 的值(用含 的代数式表示).
在 中, , 是 内一点,连接 , ,在 左侧作 ,使 ,以 和 为邻边作 ,连接 , .

(1)若 , .
①如图1,当 , , 三点共线时, 与 之间的数量关系为 .
②如图2,当 , , 三点不共线时,①中的结论是否仍然成立?请说明理由.
(2)若 , , ,且 , , 三点共线,求 的值.
在 中, , 是 内一点,连接 , ,在 左侧作 ,使 ,以 和 为邻边作 ,连接 , .

(1)若 , .
①如图1,当 , , 三点共线时, 与 之间的数量关系为 .
②如图2,当 , , 三点不共线时,①中的结论是否仍然成立?请说明理由.
(2)若 , , ,且 , , 三点共线,求 的值.
如图1,在四边形 中,若 平分 , ,且 ,则我们称这样的四边形 为“黄金四边形”, 称为“黄金角”.
【概念理解】(1)已知四边形 为“黄金四边形”, 为“黄金角”, ,若 ,则 .
【问题探究】(2)如图2,在四边形 中, , .求证:四边形 为“黄金四边形”.
【拓展延伸】(3)如图3,在“黄金四边形” 中, 为“黄金角”, ,在四边形 外部依次作△ ,△ , ,使四边形 , , 均为“黄金四边形”,且满足 , ,2, 均为“黄金角”, ,2,
①若 ,则第 个“黄金四边形”中, (用含 的式子表示).
②若“黄金角” ,则当 , , 三点第一次在同一条直线上时, .

如图 1 所示, 在四边形 中, 点 , , , 分别是 , , , 的中点, 连接 , , , , .
(1) 证明: 四边形 是平行四边形;
(2) 将 绕点 顺时针旋转得到 ,如图 2 所示, 连接 , .
①若 , ,求 的值;
②试在四边形 中添加一个条件, 使 , 的长在旋转过程中始终相等 . (不 要求证明)

在矩形 中, ,点 是 边上的任意一点(不含 , 两端点),过点 作 ,交对角线 于点 .

(1)如图1,将 沿对角线 翻折得到 , 交 于点 .
求证: 是等腰三角形;
(2)如图2,将 绕点 逆时针方向旋转得到△ ,连接 , .设旋转角为 .
①若 ,即 在 的内部时,求证:△ △ .
②如图3,若点 是 的中点,△ 能否为直角三角形?如果能,试求出此时 的值,如果不能,请说明理由.
已知正方形 中 与 交于 点,点 在线段 上,作直线 交直线 于 ,过 作 于 ,设直线 交 于 .

(1)如图1,当 在线段 上时,求证: ;
(2)如图2,当 在线段 上,连接 ,当 时,求证: ;
(3)在图3,当 在线段 上,连接 ,当 时,求证: .
如图1所示,在 中,点 是 上一点,过点 的直线与 , 的延长线分别相交于点 , .
【问题引入】
(1)若点 是 的中点, ,求 的值;
温馨提示:过点 作 的平行线交 的延长线于点 .
【探索研究】
(2)若点 是 上任意一点(不与 , 重合),求证: ;
【拓展应用】
(3)如图2所示,点 是 内任意一点,射线 , , 分别交 , , 于点 , , ,若 , ,求 的值.
