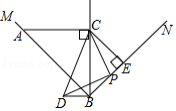
如图， ，点 是 平分线上的一点，过点 分别作 ， ，垂足分别为点 ， ， ，点 为线段 上的一点（点 不与点 、 重合），连接 ，以 为直角边，点 为直角顶点，作等腰直角三角形 ，点 落在 左侧．
（1）求证： ；
（2）连接 ，请你判断 与 的位置关系，并说明理由；
（3）设 ， 的面积为 ，求 与 之间的函数关系式．
（年湖南衡阳10分）二次函数y=ax2+bx+c（a≠0）的图象与x轴的交点为A（﹣3，0）、B（1，0）两点，与y轴交于点C（0，﹣3m）（其中m＞0），顶点为D．
（1）求该二次函数的解析式（系数用含m的代数式表示）；
（2）如图①，当m=2时，点P为第三象限内的抛物线上的一个动点，设△APC的面积为S，试求出S与点P的横坐标x之间的函数关系式及S的最大值；
（3）如图②，当m取何值时，以A、D、C为顶点的三角形与△BOC相似？
（年湖南郴州10分）已知抛物线y=ax2+bx+c经过A（﹣1，0）、B（2，0）、C（0，2）三点．
（1）求这条抛物线的解析式；
（2）如图一，点P是第一象限内此抛物线上的一个动点，当点P运动到什么位置时，四边形ABPC的面积最大？求出此时点P的坐标；
（3）如图二，设线段AC的垂直平分线交x轴于点E，垂足为D，M为抛物线的顶点，那么在直线DE上是否存在一点G，使△CMG的周长最小？若存在，请求出点G的坐标；若不存在，请说明理由．
（年湖南常德10分）如图1、2，已知四边形ABCD为正方形，在射线AC上有一动点P，作PE⊥AD（或延长线）于E，作PF⊥DC（或延长线）于F，作射线BP交EF于G．
（1）在图1中，设正方形ABCD的边长为2，四边形ABFE的面积为y，AP=x，求y关于x的函数表达式；
（2）结论：GB⊥EF对图1，图2都是成立的，请任选一图形给出证明；
（3）请根据图2证明：△FGC∽△PFB．
（2014年湖北孝感12分）如图1，矩形ABCD的边AD在y轴上，抛物线
经过点A、点B，与x轴交于点E、点F，且其顶点M在CD上．
（1）请直接写出下列各点的坐标：A ，B ，C ，D ；
（2）若点P是抛物线上一动点（点P不与点A、点B重合），过点P作y轴的平行线l与直线AB交于点G，与直线BD交于点H，如图2．
①当线段PH=2GH时，求点P的坐标；
②当点P在直线BD下方时，点K在直线BD上，且满足△KPH∽△AEF，求△KPH面积的最大值．
的值为 ．
粤公网安备 44130202000953号