初中数学作图-位似变换试题

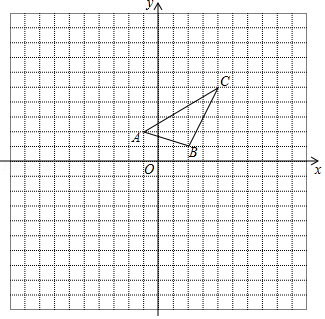
如图所示，在网格中，每个小正方形的边长均为1个单位长度，把小正方形的顶点叫做格点， $O$为平面直角坐标系的原点，矩形 $\mathit{OABC}$的4个顶点均在格点上，连接对角线 $\mathit{OB}$．

（1）在平面直角坐标系内，以原点 $O$为位似中心，把 $\mathit{\Delta OAB}$缩小，作出它的位似图形，并且使所作的位似图形与 $\mathit{\Delta OAB}$的相似比等于 $\frac{1}{2}$；

（2）将 $\mathit{\Delta OAB}$以 $O$为旋转中心，逆时针旋转 $90°$，得到△ $O{A}_1{B}_1$，作出△ $O{A}_1{B}_1$，并求，出线段 $\mathit{OB}$旋转过程中所形成扇形的周长．

如图，在边长为1的正方形网格中建立平面直角坐标系，已知 $\mathit{\Delta ABC}$三个顶点分别为 $A(-1,2)$、 $B(2,1)$、 $C(4,5)$．

（1）画出 $\mathit{\Delta ABC}$关于 $x$轴对称的△ $A_1{B}_1{C}_1$；

（2）以原点 $O$为位似中心，在 $x$轴的上方画出△ $A_2{B}_2{C}_2$，使△ $A_2{B}_2{C}_2$与 $\mathit{\Delta ABC}$位似，且位似比为2，并求出△ $A_2{B}_2{C}_2$的面积．

如图， $\mathit{\Delta ABO}$三个顶点的坐标分别为 $A(2,4)$， $B(6,0)$， $O(0,0)$，以原点 $O$为位似中心，把这个三角形的边长缩小为原来的 $\frac{1}{2}$，可以得到△ $A\text{'}B\text{'}O$，已知点 $B\text{'}$的坐标是 $(3,0)$，则点 $A\text{'}$的坐标是　　．

如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别是A（2，2），B（4，0），C（4，﹣4）

（1）请画出△ABC向左平移6个单位长度后得到的△A₁B₁C₁；

（2）以点O为位似中心，将△ABC缩小为原来的 $\frac{1}{2}$，得到△A₂B₂C₂，请在y轴右侧画出△A₂B₂C₂，并求出∠A₂C₂B₂的正弦值．

已知： $\mathit{\Delta ABC}$ 三个顶点的坐标分别为 $A(-2,-2)$ ， $B(-5,-4)$ ， $C(-1,-5)$ ．

（1）画出 $\mathit{\Delta ABC}$ 关于 $x$ 轴对称的△ $A_1{B}_1{C}_1$ ；

（2）以点 $O$ 为位似中心，将 $\mathit{\Delta ABC}$ 放大为原来的2倍，得到△ $A_2{B}_2{C}_2$ ，请在网格中画出△ $A_2{B}_2{C}_2$ ，并写出点 $B_2$ 的坐标．

如图， $\mathit{\Delta ABC}$中， $A(-4,4)$， $B(-4,-2)$， $C(-2,2)$．

（1）请画出将 $\mathit{\Delta ABC}$向右平移8个单位长度后的△ $A_1{B}_1{C}_1$；

（2）求出 $\angle A_1{B}_1{C}_1$的余弦值；

（3）以 $O$为位似中心，将△ $A_1{B}_1{C}_1$缩小为原来的 $\frac{1}{2}$，得到△ $A_2{B}_2{C}_2$，请在 $y$轴右侧画出△ $A_2{B}_2{C}_2$．

已知：如图 $\mathit{\Delta ABC}$三个顶点的坐标分别为 $A(0,-3)$、 $B(3,-2)$、 $C(2,-4)$，正方形网格中，每个小正方形的边长是1个单位长度．

（1）画出 $\mathit{\Delta ABC}$向上平移6个单位得到的△ $A_1{B}_1{C}_1$；

（2）以点 $C$为位似中心，在网格中画出△ $A_2{B}_2{C}_2$，使△ $A_2{B}_2{C}_2$与 $\mathit{\Delta ABC}$位似，且△ $A_2{B}_2{C}_2$与 $\mathit{\Delta ABC}$的位似比为 $2:1$，并直接写出点 $A_2$的坐标．

在平面直角坐标系中， $\mathit{\Delta ABC}$的三个顶点的坐标分别是 $A(1,3)$， $B(4,1)$， $C(1,1)$．

（1）画出 $\mathit{\Delta ABC}$关于 $x$轴成轴对称的△ $A_1{B}_1{C}_1$；

（2）画出 $\mathit{\Delta ABC}$以点 $O$为位似中心，位似比为 $1:2$的△ $A_2{B}_2{C}_2$．

如图，在平面直角坐标系中，已知 $\mathit{\Delta ABC}$三个顶点的坐标分别是 $A(2,2)$， $B(4,0)$， $C(4,-4)$．

（1）请在图中，画出 $\mathit{\Delta ABC}$向左平移6个单位长度后得到的△ $A_1{B}_1{C}_1$；

（2）以点 $O$为位似中心，将 $\mathit{\Delta ABC}$缩小为原来的 $\frac{1}{2}$，得到△ $A_2{B}_2{C}_2$，请在图中 $y$轴右侧，画出△ $A_2{B}_2{C}_2$，并求出 $\angle A_2{C}_2{B}_2$的正弦值．

如图，在平面直角坐标系网格中，将△ABC进行位似变换得到△A₁B₁C₁．

（1）△A₁B₁C₁与△ABC的位似比是　　；

（2）画出△A₁B₁C₁关于y轴对称的△A₂B₂C₂；

（3）设点P（a，b）为△ABC内一点，则依上述两次变换后，点P在△A₂B₂C₂内的对应点P₂的坐标是　　．

如图， $\mathit{\Delta AOB}$ 三个顶点的坐标分别为 $A(5,0)$ ， $O(0,0)$ ， $B(3,6)$ ，以点 $O$ 为位似中心，相似比为 $\frac{2}{3}$ ，将 $\mathit{\Delta AOB}$ 缩小，则点 $B$ 的对应点 $B^{\text{'}}$ 的坐标是 　      　．

如图所示的平面直角坐标系中， $\mathit{\Delta ABC}$ 的三个顶点坐标分别为 $A(-3,2)$ ， $B(-1,3)$ ， $C(-1,1)$ ，请按如下要求画图：

（1）以坐标原点 $O$ 为旋转中心，将 $\mathit{\Delta ABC}$ 顺时针旋转 $90°$ ，得到△ $A_1{B}_1{C}_1$ ，请画出△ $A_1{B}_1{C}_1$ ；

（2）以坐标原点 $O$ 为位似中心，在 $x$ 轴下方，画出 $\mathit{\Delta ABC}$ 的位似图形△ $A_2{B}_2{C}_2$ ，使它与 $\mathit{\Delta ABC}$ 的位似比为 $2:1$ ．

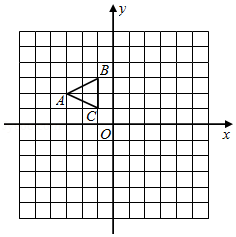
在如图所示的平面直角坐标系中，已知点 $A(-3,-3)$，点 $B(-1,-3)$，点 $C(-1,-1)$．

（1）画出 $\mathit{\Delta ABC}$；

（2）画出 $\mathit{\Delta ABC}$关于 $x$轴对称的△ $A_1{B}_1{C}_1$，并写出 $A_1$点的坐标：　　；

（3）以 $O$为位似中心，在第一象限内把 $\mathit{\Delta ABC}$扩大到原来的两倍，得到△ $A_2{B}_2{C}_2$，并写出 $A_2$点的坐标：　　．

如图，在平面直角坐标系中， $\mathit{\Delta OAB}$的顶点坐标分别为 $O(0,0)$， $A(1,2)$， $B(3,1)$（每个方格的边长均为1个单位长度）．

（1）将 $\mathit{\Delta OAB}$向右平移1个单位后得到△ $O_1{A}_1{B}_1$，请画出△ $O_1{A}_1{B}_1$；

（2）请以 $O$为位似中心画出△ $O_1{A}_1{B}_1$的位似图形，使它与△ $O_1{A}_1{B}_1$的相似比为 $2:1$；

（3）点 $P(a,b)$为 $\mathit{\Delta OAB}$内一点，请直接写出位似变换后的对应点 $P\text{'}$的坐标为　　．

给出下列结论：

①三角形的重心是三角形三条边上的中线的交点；

②圆内接四边形的对角相等；

③圆心角为，半径为4的扇形的面积是；

④在平面直角坐标系中，如果以原点为位似中心画出一个与原图形位似的图形，它与原图形的相似比为3，那么与原图形上的点对应的位似图形上点的坐标为或．

其中正确的结论是　　（填写正确结论的编号）