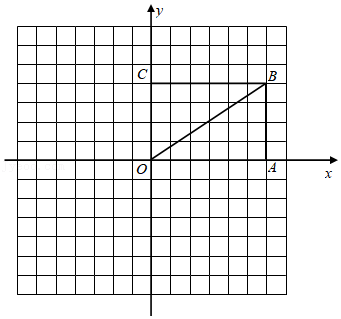
如图所示，在网格中，每个小正方形的边长均为1个单位长度，把小正方形的顶点叫做格点， 为平面直角坐标系的原点，矩形 的4个顶点均在格点上，连接对角线 ．
（1）在平面直角坐标系内，以原点 为位似中心，把 缩小，作出它的位似图形，并且使所作的位似图形与 的相似比等于 ；
（2）将 以 为旋转中心，逆时针旋转 ，得到△ ，作出△ ，并求，出线段 旋转过程中所形成扇形的周长．
六•一儿童节，小文到公园游玩，看到公园的一段人行弯道MN（不计宽度），如图，它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN（MP⊥OP，NQ⊥OQ），他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积相等，比如：A、B、C是弯道MN上任三点，矩形ADOG、矩形BEOH、矩形CFOI的面积相等. 爱好数学的他建立了平面直角坐标系（如图）.图中三块阴影部分的面积分别记为S1、S2、S3，并测得S2=6（单位：平方米），OG=GH=HI.
（1）求S1和S3的值；
（2）设T
是弯道MN上的任一点，写出y关于x的函数关系式；
（3）公园准备对区域MPOQN内部进行绿化改选，在横坐标、纵坐标都是偶数的点处种植花木（区域边界上的点除外），已知MP=2米，NQ=3米.问一共能种植多少棵花木？
如图，小明从点A出发，沿着坡度为为α的斜坡向上走了0.65千米到达点B，sinα=
，然后又沿着坡度为i=1：4的斜坡向上走了1千米达到点C．问小明从A点到点C上升的高度CD是多少千米（结果保留根号）？
在平面直角坐标系xOy中，直线
与y轴交于点A.
（1）如图，直线
与直线交于点B，与y轴交于点C，点B横坐标为
.
①求点B的坐标及k的值；
②直线与直线
与y轴所围成的△ABC的面积等于；
（2）直线与x轴交于点E（
，0），若
，求k的取值范围．
在一只不透明的布袋中装有红球、黄球各若干个，这些球除颜色外都相同，均匀摇匀.
（1）若布袋中有3个红球，1个黄球．从布袋中一次摸出2个球，计算“摸出的球恰是一红一黄”的概率（用“画树状图”或“列表”的方法写出计算过程）；
（2）若布袋中有3个红球，x个黄球．
请写出一个x的值，使得事件“从布袋中一次摸出4个球，都是黄球”是不可能的事件；
（3）若布袋中有3个红球，4个黄球．
我们知道：“从袋中一次摸出4个球，至少有一个黄球”为必然事件．
请你仿照这个表述，设计一个必然事件：．
粤公网安备 44130202000953号