[性质探究]
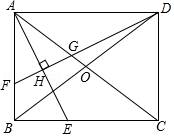
如图,在矩形 中,对角线 , 相交于点 , 平分 ,交 于点 .作 于点 ,分别交 , 于点 , .
(1)判断 的形状并说明理由.
(2)求证: .
[迁移应用]
(3)记 的面积为 , 的面积为 ,当 时,求 的值.
[拓展延伸]
(4)若 交射线 于点 ,[性质探究]中的其余条件不变,连结 ,当 的面积为矩形 面积的 时,请直接写出 的值.
相关知识点
推荐套卷
[性质探究]
如图,在矩形 中,对角线 , 相交于点 , 平分 ,交 于点 .作 于点 ,分别交 , 于点 , .
(1)判断 的形状并说明理由.
(2)求证: .
[迁移应用]
(3)记 的面积为 , 的面积为 ,当 时,求 的值.
[拓展延伸]
(4)若 交射线 于点 ,[性质探究]中的其余条件不变,连结 ,当 的面积为矩形 面积的 时,请直接写出 的值.
