初中数学相似三角形的判定与性质解答题

如图，为的直径，四边形内接于，对角线，交于点，的切线交的延长线于点，切点为，且．

（1）求证：；

（2）若，，求的值．

如图，四边形是矩形，是边上一点，点在的延长线上，且．

（1）求证：四边形是平行四边形；

（2）连接，若，，，求四边形的面积．

如图1，抛物线与抛物线相交轴于点，抛物线与轴交于、两点（点在点的右侧），直线交轴负半轴于点，交轴于点，且．

（1）求抛物线的解析式与的值；

（2）抛物线的对称轴交轴于点，连接，在轴上方的对称轴上找一点，使以点，，为顶点的三角形与相似，求出的长；

（3）如图2，过抛物线上的动点作轴于点，交直线于点，若点是点关于直线的对称点，是否存在点（不与点重合），使点落在轴上？若存在，请直接写出点的横坐标，若不存在，请说明理由．

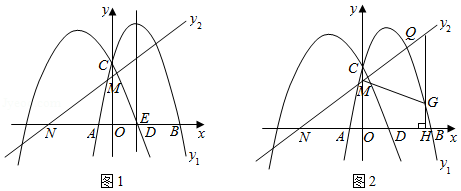
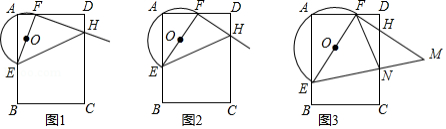
如图，在正方形中，，点在边上，连接，作于点，于点，连接、，设，，．

（1）求证：；

（2）求证：；

（3）若点从点沿边运动至点停止，求点，所经过的路径与边围成的图形的面积．

如图，内接于，是直径，，与相交于点，过点作，垂足为，过点作，垂足为，连接、．

（1）求证：直线与相切；

（2）若，求的值．

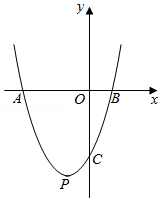
如图，抛物线与轴交于，两点，与轴交于点，抛物线的顶点为．已知，．请答案下列问题：

（1）求抛物线的解析式，并直接写出点的坐标；

（2）抛物线的对称轴与轴交于点，连接，的垂直平分线交直线于点，则线段的长为　　．

注：抛物线的对称轴是直线，顶点坐标是，．

如图，在平面直角坐标系中，四边形的边在轴上，在轴上．为坐标原点，，线段，的长分别是方程的两个根，．

（1）求点，的坐标；

（2）为上一点，为上一点，，将翻折，使点落在上的点处，双曲线的一个分支过点．求的值；

（3）在（2）的条件下，为坐标轴上一点，在平面内是否存在点，使以，，，为顶点四边形为矩形？若存在，请直接写出点的坐标；若不存在，请说明理由．

如图，在中，，以为直径的交于点，连接，过点作，垂足为，、的延长线交于点．

（1）求证：是的切线；

（2）求证：；

（3）若，，求的长．

证明：（1）如图，连接，

是直径，

，

又，

，，

，，

，

，

，

又是半径，

是的切线；

（2），

，

，，

，

，

，

又，

，

，

；

（3），，

，

，

，

，

，

，

，

，，

，

，

，

．

古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的是圆”．请研究如下美丽的圆．如图，线段是的直径，延长至点，使，点是线段的中点，交于点，点是上一动点（不与点，重合），连接，，．

（1）求证：是的切线；

（2）小明在研究的过程中发现是一个确定的值．回答这个确定的值是多少？并对小明发现的结论加以证明．

如图，在中，以为直径的交于点，连接，且，连接并延长交的延长线于点，与相切于点．

（1）求证：是的切线；

（2）连接交于点，求证：；

（3）若，求的值．

背景：一次小组合作探究课上，小明将两个正方形按如图所示的位置摆放（点 $E$ 、 $A$ 、 $D$ 在同一条直线上），发现 $\mathit{BE}=\mathit{DG}$ 且 $\mathit{BE}\perp \mathit{DG}$ ．

小组讨论后，提出了下列三个问题，请你帮助解答：

（1）将正方形 $\mathit{AEFG}$ 绕点 $A$ 按逆时针方向旋转（如图 $1)$ ，还能得到 $\mathit{BE}=\mathit{DG}$ 吗？若能，请给出证明；若不能，请说明理由；

（2）把背景中的正方形分别改成菱形 $\mathit{AEFG}$ 和菱形 $\mathit{ABCD}$ ，将菱形 $\mathit{AEFG}$ 绕点 $A$ 按顺时针方向旋转（如图 $2)$ ，试问当 $\angle \mathit{EAG}$ 与 $\angle \mathit{BAD}$ 的大小满足怎样的关系时，背景中的结论 $\mathit{BE}=\mathit{DG}$ 仍成立？请说明理由；

（3）把背景中的正方形分别改写成矩形 $\mathit{AEFG}$ 和矩形 $\mathit{ABCD}$ ，且 $\frac{\mathit{AE}}{\mathit{AG}}=\frac{\mathit{AB}}{\mathit{AD}}=\frac{2}{3}$ ， $\mathit{AE}=4$ ， $\mathit{AB}=8$ ，将矩形 $\mathit{AEFG}$ 绕点 $A$ 按顺时针方向旋转（如图 $3)$ ，连接 $\mathit{DE}$ ， $\mathit{BG}$ ．小组发现：在旋转过程中， $D{E}^2+B{G}^2$ 的值是定值，请求出这个定值．

如图，抛物线 $y=\frac{3+\sqrt{3}}{6}{x}^2+\mathit{bx}+c$ 与 $x$ 轴交于 $A$ ， $B$ 两点，点 $A$ ， $B$ 分别位于原点的左、右两侧， $\mathit{BO}=3\mathit{AO}=3$ ，过点 $B$ 的直线与 $y$ 轴正半轴和抛物线的交点分别为 $C$ ， $D$ ， $\mathit{BC}=\sqrt{3}\mathit{CD}$ ．

（1）求 $b$ ， $c$ 的值；

（2）求直线 $\mathit{BD}$ 的函数解析式；

（3）点 $P$ 在抛物线的对称轴上且在 $x$ 轴下方，点 $Q$ 在射线 $\mathit{BA}$ 上．当 $\mathit{\Delta ABD}$ 与 $\mathit{\Delta BPQ}$ 相似时，请直接写出所有满足条件的点 $Q$ 的坐标．

已知：在矩形中，，分别是边，上的点，过点作的垂线交于点，以为直径作半圆．

（1）填空：点　　（填“在”或“不在” 上；当时，的值是　　；

（2）如图1，在中，当时，求证：；

（3）如图2，当的顶点是边的中点时，求证：；

（4）如图3，点在线段的延长线上，若，连接交于点，连接，当时，，，求的值．

如图，点是线段上一点，，以点为圆心，的长为半径作，过点作的垂线交于，两点，点在线段的延长线上，连接交于点，以，为边作．

（1）求证：是的切线；

（2）若，求四边形与重叠部分的面积；

（3）若，，连接，求和的长．

如图1，在平面直角坐标系中，已知抛物线与轴相交于、两点（点在点的左侧），与轴交于点．

（1）点的坐标为　　，点的坐标为　　，线段的长为　　，抛物线的解析式为　　．

（2）点是线段下方抛物线上的一个动点．

①如果在轴上存在点，使得以点、、、为顶点的四边形是平行四边形．求点的坐标．

②如图2，过点作交线段于点，过点作直线交于点，交轴于点，记，求关于的函数解析式；当取和时，试比较的对应函数值和的大小．